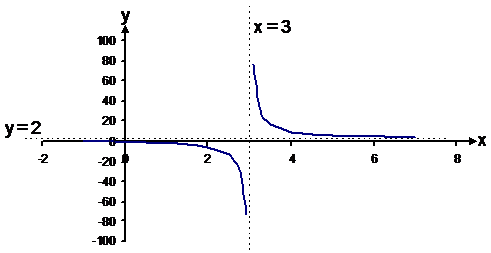
Some graphs are not defined for all values of x.  By not defined, we mean there is no y-value for that x-value.

The following function is undefined at x = 3:

                                                         

When x = 3, the denominator is equal to 0, so we have:

                                                   

This is undefined. Since there is a point where y is not defined, we can say that this function is discontinuous at x = 3. This means it does not have a y-value for every x-value. To plot a function like this, you need to look at a few things. 

Firstly, you find where the function is undefined – in this case at x = 3.  Then you work out what sort of value the function has at four points:

Approaching :

                                                       

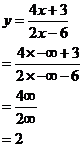
The 3 and the –6 can be ignored as they are insignificant when compared with .

Approaching   from the negative side:

                                        

Approaching   from the positive side:

                                         

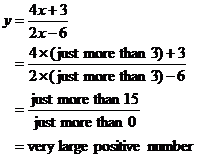
Approaching :

                                                       

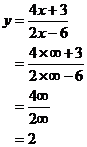
Now, I can use this to plot my function near these points:

·         Towards , y approaches 2.  Approaching x = 3, from the negative side, y approaches a very large negative number.  So when I travel right from  towards x = 3, my function is getting more negative – it is decreasing.

·         Towards , y approaches 2 again.  However, approaching x = 3 from the positive side, y approaches a very large positive number.  So if I travel left from  to x = 3, my function is getting more positive – it is increasing.

With this in mind, I can draw the function around these four points.  Since I can’t draw it all the way to  or , I just go a reasonable distance from the y-axis.

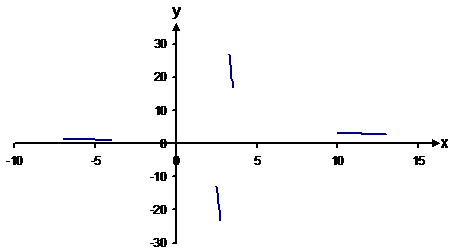
Now it is just a simple task of joining up the lines. Since the function is undefined at x = 3, you can draw a vertical dotted line there – a vertical asymptote. 

You can also draw a horizontal asymptote at y = 2 since y does not actually ever get to 2.