Turning recurring decimals into fractions
Often in problems you get a decimal answer that is recurring. This means that the decimal part of the number contains a sequence that repeats over and over again. An example is the number 5.23232323… which has the number sequence ‘23’ repeating over and over again. Often you need to write such a number as a fraction. There is an easy method for doing this.
Sponsored Links
Write down the number first, making sure to include a few repeats of the sequence:
5.23232323…
Let’s also call this number ‘x’:
![]()
Multiply the number so that one sequence of the repeating numbers is to the left of the decimal point. In this case, we have to multiply it by 100 to achieve this:
![]()
Now, take the first number away from the second number:
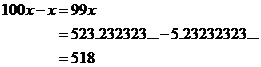
The decimal parts of both numbers cancel out, and all you are left with is 523 – 5 = 518, which is 99x.
So we have 99x = 518. We wanted our number in a fraction form, so we want to know what one x is. We simply divide the 518 by 99 and get 518/99 as our fraction. This is an improper fraction, since the numerator (number on top) is larger than the denominator (number on the bottom). In proper fraction form, it is 5 + 23/99.
Let’s try it with something harder, say 32.746746746… the repeating sequence is ‘746’. Also remember we call this number ‘x’.
To get one sequence on the left of the decimal point we need to multiply by 1000.
Doing this we get 32746.746746… which is also 1000x.
![]()
Subtract the first number from the second:
The decimal parts cancel out and we get:
![]()
This is also:
![]()
So we have 999x = 32714. We want to know what one x is, so we divide 32714 by 999. This gives us in fraction form, 32714/999. In proper fraction form it is:
![]()

