Finding polynomial relationships

Sometimes you’re given some data about a mathematical relationship between two variables, without actually being given the relationship itself.  For instance, you might be told that there is some relationship between the variables ‘x’ and ‘y’.  Now, there’s a technique called finite differences that can help you find the polynomial relationship that describes or fits the data.  It won’t give you the actual relationship directly, but it will tell you what degree the polynomial is.  Remember that the degree of a polynomial is about what the highest power of the variable in it is.  Say we had the following data about x and y values:

What we can do is work out the differences between each of the y values.  For example, the difference between ‘–1’ and ‘2’ is ‘3’.  We can write these differences to the right of the y values, like this:

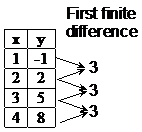
This new column we’ve added to our data is known as the first finite difference column.  Notice how all the values are the same – they’re all ‘3’.  To do the finite difference method, we need to keep taking differences until we get to a column with all the same values in it.  How many columns this takes tells us what the order of the relationship is.  In this case, we’ve reached all the same values in the first finite difference column.  This tells us that our relationship is a first order relationship – a linear one.

This is confirmed when I reveal that the relationship I used to generate the table of values was:

                                                         

The highest order of ‘x’ in this expression is ‘1’ – it’s a first order polynomial.  So the finite difference method can tell us what order the relationship that describes the data is.

To avoid getting too messy, I like to use a table to do the whole finite difference method, rather than using arrows.  For this last example, my table would have looked like this:

I write the difference between any two values in the cell to the right of the bottom value.  So for instance, when I calculate the difference between ‘–1’ and ‘2’, I write the answer to the right of the ‘2’.

You can also use the finite difference method to find out about higher order relationships.  For instance, try it for this data:

 

We can calculate the set of first finite differences. The difference between 8 and 15 is 7, the difference between 15 and 28 is 13, and so on:

Notice how the values in the first finite difference column aren’t the same.  This tells us that the relationship is not a first order or linear one.  Let’s keep going and find the set of second finite differences.  We can do this by finding the differences between the values in the first finite differences column:

Bingo!  The values in the second finite difference column are all the same.  This tells us that the relationship between y and x is a second order relationship.

Using finite differences to find the actual relationship

Say we have a general linear equation, like this:

                                                         

We can use the finite differences method on it just like any other equation.  First we start off with some x and y values:

Then we do the finite differences method:

We know that  is a first order (or linear) equation, and this is confirmed when we get all the same values in our first finite difference column.  What’s more interesting are these two things:

·         The y value when ‘x = 0’ is the value of ‘b’ in our general equation

·         The values in the first finite difference column are the values of ‘a’ in our general equation

If we go back to our original linear equation example, and add in  row, we get:

Now, since the values are all the same in the first finite difference column, this means the relationship between x and y is a linear one.  The general form of the relationship is going to be .  But, we can get our ‘a’ and ‘b’ values directly from the table.  ‘a’ is the value in the first finite difference column – so .  ‘b’ is the value when .  So that means .  So our equation is:

                                                         

This matches with what the actual equation was.

You can also do the same for a second order equation.  The general form of a second order equation is:

                                                    

If we run this equation through the finite difference method, we get something like this:

We have to go to the second finite difference column before we get all the same values in the column.  This confirms that the relationship between x and y is a second order one.  What’s more interesting now is that all the values in the second finite difference column are ‘2a’.  So any value we get in that second finite difference column is going to equal ‘2a’.  If you look at the top entry in the first finite difference column, it’s ‘a + b’.  If we’ve already worked out ‘a’, then we can work out ‘b’ from this.  Lastly, the value of ‘c’ is just going to be the value of ‘y’ when ‘x = 0’.

If we go back to the quadratic example from earlier, and add in an ‘x = 0’ row, we get:

We also know that this is a second order relationship, so it’s going to fit the general form:

                                                    

We know the values in the second finite difference column are all equal to ‘2a’.  So:

                                                            

Also, we know that the top value in the first finite difference column is going to equal ‘a + b’.  So:

                                                        

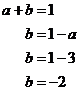
And last of all we can work out the value of ‘c’ by looking at the value of ‘y’ when ‘x = 0’:

                                                             

So our overall relationship is:

                                                    

 

 

 

The values in the rightmost finite difference column are always the same all the way down the column. They depend only on the range of x values and the order of the relationship. For instance, a first order relationship with x values going 0, 1, 2, 3… will have ‘a’ all down the first finite difference column. If the x values go 0, 3,