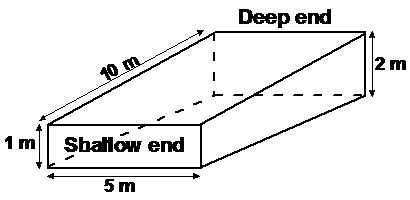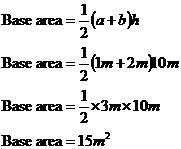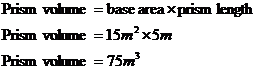Prisms are a type of solid shape. To be a prism a shape has to have a few characteristics. First of all, a prism has two faces that are identical in shape and are parallel. These two faces are sometimes called the bases of the prism. Between these two faces are the rest of the sides of the prism – these sides or faces are usually rectangles.
Prisms are usually named based on the shape of the two parallel faces. For instance, a prism with two parallel square faces would be known as a “square based prism” or sometimes just “square prism”. A prism which had triangular parallel faces would be called a “triangle based prism” or just “triangular prism”.
Sponsored Links
Here are some prisms:
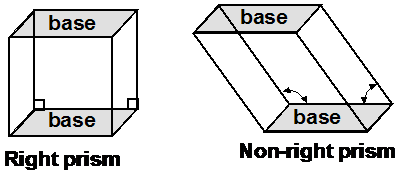
These prisms in the diagram above are known as right prisms because all the sides are at right angles to the bases. You can also get non-right prisms, where the sides are not at right angles to the bases. Here are two versions of a rectangular prism – a right prism version and a non-right prism:
It’s really easy to find the volume of right prisms. All you have to do is find the area of the base of the prism, and then multiply this by the length of the other sides of the prism:
For instance, say we had to work out the volume of this triangular prism:
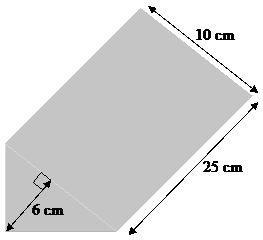
The base of this prism is a triangle. We know that
the formula for the area of a triangle is 
. So we just need to work out what
the base area and the height of the triangle are. This is where it sometimes
gets a bit tricky – the triangle may be rotated to a different orientation then
what you’re used to seeing. So which out of the 10 cm and the 6 cm measurement
is the base? Well, the base of the triangle is a side of the triangle,
and only the 10 cm measurement is along a side. So ‘b’ is 10 cm. Now what
about height? The height of a triangle is the distance across the triangle in
a direction perpendicular to the base. Perpendicular means, “at right angles
to,” if you don’t remember. The 6 cm measurement fits this definition, so ‘h’
is 6 cm. We can plug these values in:
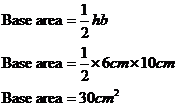
So now that we have the area of the base, to get the prism volume all we need to do is multiply this area by the length of the prism, which is 25 cm:
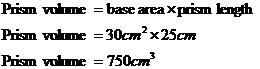
Remember to check that you’ve got the right units – a volume is measured in cubic units, so we expect whatever the unit is to be raised to the power 3. We’re using centimetres, and it is raised to the power 3, so we’ve got the units OK.
Cylinders
A cylinder is like a prism because it has two bases that are identical shapes and are parallel to each other. However, it only has one side that connects these two bases, and this side isn’t flat – it’s curved. The base shape of a cylinder is a circle. Like prisms, you can have right cylinders and non-right cylinders.
Finding the volume of a right cylinder is just like for a prism. First you find the area of the base, which is always a circle for a cylinder. Then you multiply this area by the height or length of the cylinder.
Practical prism questions
There are a lot of questions based on doing stuff in the real world that involve finding the volumes of prisms. One of the tricky parts about doing these questions is sometimes working out which faces or sides of a solid shape are the bases. What you’re looking for are two faces that are congruent – the same shape and the same size, and also parallel to each other.
|
Jenny is digging a hole in her backyard for a new, in ground pool (in ground means the pool is sunk into the ground rather than being a structure above the ground). It’s a normal sized family pool, rectangular in shape, with a shallow end and a deep end. It’s 10 metres long, 5 meters wide, 2 metres deep at the deep end and 1 metre deep at the shallow end. What volume of dirt is Jenny going to have to remove? |
|
Solution |
|
First things first – let’s draw a diagram:
Now are there any identical faces that are parallel to each other? What about the top and bottom faces? Are they parallel to each other? It turns out they’re not quite parallel to each other – the top face is flat like the ground around the pool, but the bottom face (which is the bottom of the pool) is sloping slightly. It slopes slightly downwards going from the shallow end to the deep end. Are they identical? If you look closely, you can see that the bottom of the pool is going to be slightly longer than the top side of the pool. So they’re not identical either. What about the deep end and shallow end sides? Are they parallel – yes! They’re both rectangles, but they’re not the same size – the shallow end is a 1 metre by 5 metre rectangle, but the deep end is a 2 metre by 5 metre rectangle. So this leaves the other two faces of the pool – the long sides of the pool. Are they parallel – yes! Are these the same shape and size – yes! They’ve both got this shape and size:
Now in order for us to be able to work out the entire volume of the pool, we need to know the area of this shape. So what type of shape is it? Well, the one metre and two metre sides are parallel to each other. The whole shape has four sides. This is enough information for us to be able to class it as a trapezium. The area of a trapezium is All we need to do is multiply this base area by the length of the prism. Now don’t make the mistake of going, “the length of the prism is 10 metres so I’ll multiply the base area by this.” Yes, the pool is 10 metres long. But this is not the length of our prism. The length of our prism is the distance between its two bases, which is 5 metres:
So to get the total volume of the pool: So Jenny will have to dig out 75 cubic metres of dirt to make room for the pool. She’s gonna need to hire a bobcat or mechanical shovel to do the work – with a shovel even digging up one cubic metre of earth is a huge effort, let alone 75 cubic metres. |
, where ‘a’ and ‘b’ are
the lengths of the two parallel sides. ‘h’ is the height of the trapezium,
the perpendicular distance between the two parallel sides. So ‘a’ and
‘b’ in this case are ‘1 m’ and ‘2 m’, and ‘h’ is ‘10 m’. Notice how the 10
metre side is exactly at right angles to the 1 and 2 metre sides – it is perpendicular
to these sides. This is why we choose it as ‘h’. So the area of the
trapezium is:
