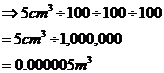3D solid shapes
3D shapes are ‘solid’ – if you made a three-dimensional shape it would take up space wherever it was placed. These are some examples of 3D shapes:


Sponsored Links
A lot of objects in everyday life are three-dimensional shapes – a lunchbox, a bottle of water, or a brick are all solid shapes.
These solid shapes take up or occupy space in the world – the amount of space an object takes up is known as its volume. In terms of everyday items, say we compare a water bottle to a fridge. The bottle only takes up a small amount of space – it has a small volume. The fridge on the other hand takes up a large amount of space – it has a large volume. So that’s how we use the word.
Units of volume
We measure lengths or distances in ‘normal’ units – metres, or centimetres, or kilometres. For areas we use square units – so metres squared (m2), or centimetres squared (cm2) etc. Well for measuring volume, we go up to cubic units – units raised to the power 3. So we measure volumes in metres cubed (m3) or centimetres cubed (cm3). Why do we do this? Well, how about we look at a simple cube shape (a cube is a shape like a die):


When you’re measuring the length of a line, you only have one dimension to measure – how long it is. With a two-dimensional shape however, you have two dimensions – length and width. Or perhaps length and height in some cases, it just depends on what names you use.
When you measure a three-dimensional object, you’ve got to measure three things – the length, width and height. These are the usual names for the three dimensions, although sometimes you may get other names – ‘thickness’ for instance. But anyways, the point is there are three different dimensions in a solid shape.
So back to our cube – how do we work out its volume? Well, we just need to multiply its three dimensions together. So, we need to multiply its length by its height by its width. Because it’s a cube, the length, height and width are all the same value. In this case, they’re all 1 cm. So the calculation is:
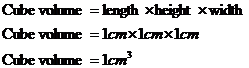
Remember when you multiply something by itself (in this case ‘cm’ by ‘cm’) it becomes ‘cm’ to the power 2, or cm2. If you multiply it by itself again, then you get ‘cm’ to the power 3, or cm3.
Changing between units of volume
There are very big differences between different units of volume. A cubic centimetre is a lot bigger than a cubic millimetre, even though we know there are 10 millimetres in a centimetre. Let’s see why there’s such a huge difference, by looking at a cubic centimetre:

Each side of this cube is 1 centimetre long, or 10 mm long. So along one edge of the cube, you can fit 10 ‘lots’ of 1 mm. But in the entire volume occupied by the cube, how many lots of 1 mm3 can you fit? Well, in the diagram, each little cube is a 1 mm by 1 mm by 1 mm cube. How many of them are there? If we can fit 10 lots of 1 mm along one side of the cube, and 10 lots of 1 mm along another side of the cube, then we can fit 10 x 10 or 100 cubic millimetres in one layer:


How many of these layers are there? Well each layer is 1 mm thick. The cube is 10 mm high, so this means there are 10 layers. With 100 mm3 cubes in a layer, this means there are 10 x 100 or 1000 mm3 total in a cubic centimetre.
So 1 cm3 = 1000 mm3. In general, to convert between one unit of volume and another, you need to do the conversion as if you were converting between different lengths, but do it three times. Say I was changing from 5 cm3 to m3. Normally, to convert from a length in centimetres to a length in metres, I’d just divide by 100. Well, for volumes, I need to do it three times. So I’d go: