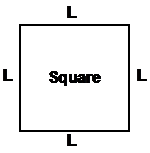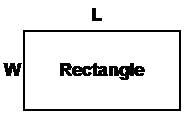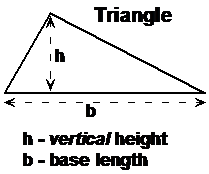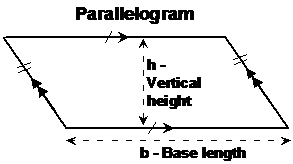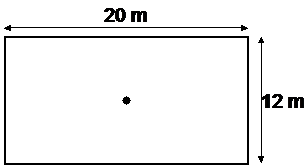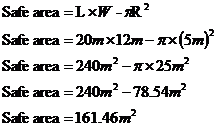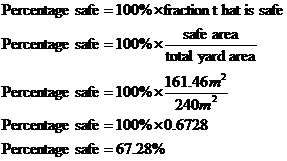The formulas to work out the areas of most shapes are fairly simple. However, the best way to learn them is to understand how the formulas were created in the first place. By doing this, even if you forget the exact formula in an exam you can usually work it out for yourself! So here are some brief explanations about how each formula was created for each shape.
Area of a triangle
Sponsored Links
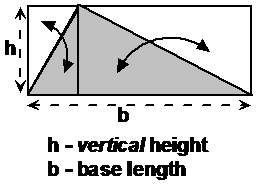
If you draw a triangle like the shaded area in the diagram you can always draw a rectangle around it like in the diagram. Look how the triangle (the shaded area) can be split into two separate bits. Each of those bits has a matching area in the rectangle. The matching areas are shown by the double headed arrows in the diagram.
We already know that the total area of a rectangle is just the length multiplied by the width. In this diagram we’ve got different symbols to L and W – instead we’ve got ‘b’ and ‘h’. So the area of our rectangle is just ‘b’ multiplied by ‘h’ – ‘bh’. Now what fraction of this area is taken up by the triangle? Well, the triangle takes up exactly half of the area of the rectangle. This is because each bit of the triangle has another matching bit in the rectangle. If you wanted to you could take the part of the rectangle which isn’t in the triangle and make another triangle like this:
This diagram shows how you can rotate the remaining
bits of the rectangle around to make another identical triangle. This demonstrates
that two of these triangles fit inside the rectangle. This means that the area
of each triangle is half of the rectangle’s area. So if the rectangle’s area
is ‘bh’, then the triangle’s area is 
. Be careful to use the vertical
height in your calculations, like it’s labelled in the first diagram.
Area of a parallelogram
It’s easy to cut a bit off a parallelogram and move it to the other side so that you get a rectangle. We all know the area of a rectangle is just its length multiplied by its height or width. So the area of a parallelogram is just its vertical height multiplied by the length of one of the parallel sides.
Area of a trapezium
A trapezium has four sides, with two of the sides parallel. Like for a triangle and parallelogram, you can calculate its area by putting a rectangle over it and re-arranging bits like this (you might need to rotate the bits to make them fit):
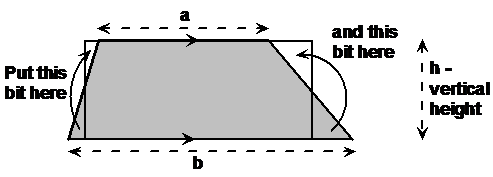
So what you get by re-arranging these two bits is a
rectangular area. The height of the rectangle is the same as the vertical
height of the trapezium, but how long is its other side? Well, it’s longer
than ‘a’, but shorter than ‘b’. In fact, it’s exactly halfway between ‘a’ and
‘b’ in length – so it’s the average of ‘a’ and ‘b’. The average of ‘a’ and ‘b’
is half of them added together: 
. So the area of a trapezium is just
this length times the vertical height:
Area of a circle
There are a few ways to work out the area of a
circle. Like for most of the other shapes, it involves cutting up the shape
and re-arranging it. In this case, we need to cut the circle up into lots of
little wedges, just like you were cutting a cake. Then we can pull out these
wedges one by one and line them up like in the diagram. Now, we know that the
circumference or perimeter of the circle is 
, this is shown in the diagram around
the circle. When we line up the wedges, the length of the side made up of all
the wedge ends is also going to be the same length - . The height of this row
of lined up wedges is going to be the radius of the circle – R. The 
symbol is the
lowercase version of the capital symbol for pi, which is 
.
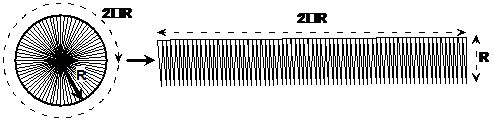
Now what we can do is split this line of wedges up
into two parts, and then flip one vertically and push it against the other
one. This will halve the length of the rows to just 
:
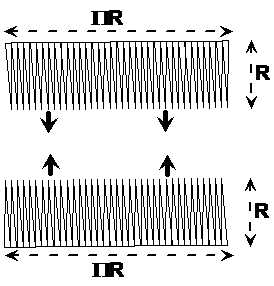
When they get pushed together, you just get a rectangle:
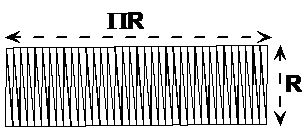
Now we all know that the area of a rectangle is its length multiplied by its height. So in this case, it’s:
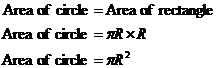
And that’s how you get the formula for the area of a circle.
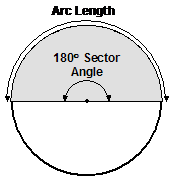
Area of a sector
A sector is a pie shaped wedge of a circle. To work out what its area is, we just need to find out what fraction of the circle the sector is occupying. Now we’ve already worked out that a sector with a sector angle of 360° is the same as a circle. This means it would have the same area as the whole circle. What about a sector angle of 180°? Well this would only be half a circle, so it would only have half the area of a circle.
|
|
|
So the fraction of the circle area that the sector takes up is just the sector angle divided by the angle you’d need to get a sector like a circle, which is 360°. In mathematical terms, the formula for the area of a sector is:
Now we know that the area of a circle is 
, and we’ve just
worked out that the fraction of the circle the sector occupies is the sector
angle divided by 360°. So we can rewrite the formula:
Here is a summary of some area formulae:
|
|
Area = L2 |
|
|
Area = L × W |
|
|
Area = |
|
|
Area = |
|
|
Area = bh |
|
|
Area = |
Things to watch out for
There are only a few tricky things to look out for when you’re doing simple area questions. First of all, sometimes questions will mix units – so for instance they might have centimetres and metres in the same question. Make sure you work using only one type of unit – so you may have to convert one of the units into another type. For instance, if you chose to work in centimetres, you’d have to convert all metre lengths into centimetres by multiplying by 100.
Second thing you have to watch out for is problems which have a combination of shapes in them – a question may have both rectangles and circles in them. Also, sometimes you’ll only get parts of shapes, rather than the whole shape.
|
This is a classic problem which you’re sure to come up against in an exam one day. Also, if you’ve got a pet dog it is a somewhat useful question to answer too! Here it is: Wolfie the dog is tied up to a stake in the centre of a rectangular yard. Unfortunately you’ve also let Bertie your pet mouse out in the yard too, and Wolfie’s doing everything he can to get him! The rope Wolfie’s tied up with is 5 metres long, and the yard is 12 metres wide and 20 metres long? What percentage of the yard is safe for Bertie to be in? |
|
Solution |
|
Okay, first thing with any of these questions – draw a diagram! This means you have to read and understand the question, and identify what the important bits of information are. In this question – the yard’s a rectangle, and it’s 12 metres by 20 metres. Wolfie is tied to a stake in the centre of the yard – so let’s draw that as well:
Now Wolfie’s on a 5 metre rope. Whenever you have something tied to a fixed object, the area that it can reach is circular in shape, and the radius of the circle is the length of the rope it’s tied with. So in this case, the part of the yard that Wolfie can get to is a circular area of radius 5 metres. So we can add this to the diagram:
It’s important to draw the diagram roughly to scale. This will give you an idea of whether your answer makes some sense. For instance, looking at the diagram, I would expect that the safe area for Bertie is going to be something between 40% and 80% of the yard. We want to work out what percentage of the yard is safe for Bertie. We can do this by first working out the safe area for Bertie, and then working out what percentage of the whole yard this is. The safe area for Bertie is the area of the yard which doesn’t include the area Wolfie can reach. We can write a mathematical expression: The whole yard area is a rectangle, which we can work out the area for. The area Wolfie can reach is a circle, which we can also work out the area for. First we need to write in the formulas for the areas: The length of the yard is 20 metres – L. The width of the yard is 12 metres – W. And the radius of the circle is 5 metres – R. So: This is the safe area. Now all we have to do is work out what percentage of the entire yard this is. This is easy to do: Does this answer make sense? Well from our diagram it looks like the safe area is more than half of the total area, but by no means all of it either, so 67.28% seems like a reasonable answer. |
