Now we know lots of two dimensional shapes – squares, circles, rectangles, triangles, parallelograms and more.  There is a general name for any plane shape which has straight sides and is a closed shape – a ‘polygon’.  Now in order to actually be a shape, it has to have at least 3 sides.  But that’s the only restriction – polygons can have as many sides as you want.  There are however some names for some of the more common polygons, based on how many sides they have:

There are several different types of polygons, depending on how they look.  Here they are:

Regular polygons

These are the nice looking polygons.  There are two important things to remember about regular polygons:

·         All their sides are the same length

·         All their interior angles are the same

If a shape you’re looking at is a regular polygon, you can describe it by saying it is a “regular…” followed by the name for a shape with that many sides.  For instance, this is a regular octagon:

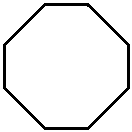
Irregular polygons

Any polygon which isn’t a regular polygon is an irregular polygon.  To work out what an irregular polygon is like, you just need to reverse the rules for a regular polygon:

·         Has at least two sides of different length

·         Has at least two different sized interior angles

Concave polygons

To remember what concave means it’s best to split the word up like this – “con” + “cave”.  The important part is the “cave” part – the word concave is used to describe shapes that have something looking like a cave in them.  When you talk about concave polygons, the cave is on the outside of the polygon.  Another way of spotting concave polygons is to look out for any interior angles that are larger than 180°.  Remember that angles larger than 180° are called reflex angles. 

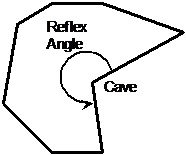
Convex polygons

These are sort of the opposite of concave polygons.  Convex polygons don’t have any ‘caves’ on their outsides, and none of the interior angles are larger than 180°.  Most people find convex polygons look a lot more ‘normal’.

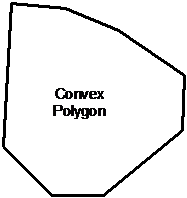
Deriving the formula for the sum of the angles inside a polygon

The word ‘deriving’ often scares people, and sometimes they’ve got a right to be scared.  Deriving and proving formulas and theorems can often be hard work.  You’ve probably heard of the famous equation by Einstein:

                                                          

But think about the process that he had to go through to get this equation.  A lot of work went into coming up with it.  Luckily, some formulas and theorems are pretty easy to prove.  Here we’ll show you how to get a theorem telling you an easy way to work out the sum of all the angles inside a polygon.

First up, here’s the theorem:

                                   

‘n’ is the number of sides that the polygon has.

Now sometimes in exams you may be asked to prove a theorem which you are given, like this one.  To prove the theorem, you need to think about what you know in mathematics that you might be able to apply to this situation.  Let’s run through proving this angle theorem:

First you may want to express the theorem in your own words.  For me it’d come out something like:

So you take your polygon and count the number of sides.  You take two away from that, and then multiply by 180°.  The answer you get is the sum of all the angles inside the polygon.

Now you look for anything ‘suspicious’ in the theorem which might give you a clue to how to prove it.  There’s the ‘n – 2’ part, but taking away 2 from something doesn’t ring any alarm bells.  What about the ‘180°’?  It’s definitely a ‘special’ angle – it’s called a straight angle.  What else is special about it?  Well, think triangles.  The sum of all the angles inside a triangle is 180°.  This seems a bit much of a co-incidence.  So we need to investigate our hunch.  The theorem works with any polygon, so let’s draw one:

Now, we think the theorem might have something to do with triangles.  How can we work triangles into the diagram?

One way is to start at a corner and draw a line to another point like this:

Aha!  We’ve created a triangle.  But wait!  We can create more triangles if we continue drawing lines to the other corners:

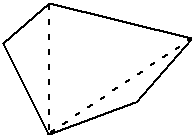
So now we’ve got three triangles in the inside of this polygon.  Our theorem tells us about the sum of all the angles inside a polygon.  What we’ve got here is our polygon split up into three triangles.  But we know that the angles inside a triangle add up to 180°.  And we’ve got three triangles in this case.  So the total angles inside this polygon must be .

We’ve worked out the sum of the angles for this polygon.  What about generally?  Well, once we know how many triangles fit into any polygon, we can work out the sum of all the angles inside.  Now polygons with different numbers of sides will have different numbers of triangles inside them.  For instance, a quadrilateral only has two triangles inside it:

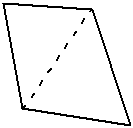
So to prove the theorem, we need a general way of saying how many triangles there are going to be inside a polygon.  The theorem once again gives us a clue about how to do this – it has the number of sides in it as a variable ‘n’.  So maybe we can say how many triangles there are inside a polygon based on the number of sides.

The quadrilateral has four sides and two triangles.  The pentagon before it had five sides and three triangles.  See the trend?  Take the number of sides, subtract two, and you get how many triangles fit inside the polygon.  So:

                               

Each triangle has 180° in it.  So to get the total sum of angles inside the polygon, we need to multiply the number of triangles by 180°:

                        

And there’s how to show the theorem is correct.  For peace of mind you may want to check that the theorem works for one or two polygons.  Let’s try a triangle, which we know has 180° worth of angles inside it.  A triangle has 3 sides, so n = 3:

                                   

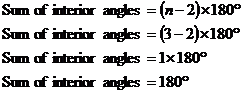
It gets that right, which gives us a bit of an indication the theorem is correct and works.  When you’re checking a theorem, it’s often best to use things you haven’t used to prove the theorem.  In our case, we used a quadrilateral and a pentagon to prove the theorem.  So to check it we used a polygon with a different number of sides to these – a triangle.

Tessellations

If you take any shape and repeat it over and over again you can make quite a pretty pattern.  Tessellations are patterns of shapes which completely cover an area.  This means that there are no gaps or holes left in-between shapes.  Tessellations don’t have to use only one shape.  Some of the more beautiful ones have several different shapes in them.  Simple tessellations are easy to draw or make – such as ones using squares:

More complicated combinations of shapes can be tessellated.  You might get a question asking you to tessellate an octagon and a diamond shape together.  The trick to doing this is to play with different sized shapes and draw them in different orientations until you see one which will work as a tessellation.  For instance, this doesn’t work:

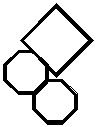
But after a bit more playing around you might get something like:

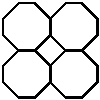
This works, and can be expanded as much as you want: