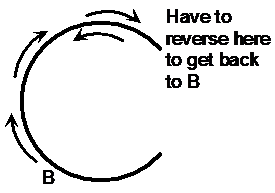2D shapes
2D stands for two-dimensional. 2D shapes are ‘flat’ shapes – they are shapes you can cut out of a flat sheet of paper. A page of this book is an example of a 2D shape – it is a rectangle.
These are some examples of two-dimensional shapes:
Sponsored Links

2D shapes are often called plane shapes. The ‘plane’ part is to do with how you can represent these shapes using a plane – which is a flat area. For example, you can make a rectangle out of a piece of paper by cutting it out. But if you wanted to make a cube, you’d have to fold the paper and make a solid shape. It would no longer be a plane shape.
Quadrilaterals
Quadrilaterals are shapes with exactly four straight sides. They also have exactly four corners. The interior angles of any quadrilateral add up to 360°. There are lots of special types of quadrilaterals – here are some of them:
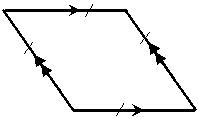
Parallelograms
A parallelogram is a quadrilateral – it has four sides and four corners. However, it also has some special characteristics. Each pair of opposite sides is parallel to each other. Here’s a typical parallelogram:
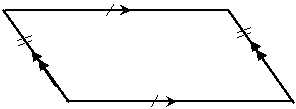
Notice that each side is parallel with the side opposite it. Also, the lengths of opposite sides in a parallelogram are the same.
The rectangle
A rectangle is a type of parallelogram, with all the interior angles exactly 90°.
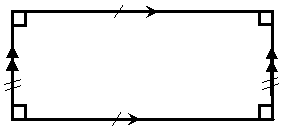
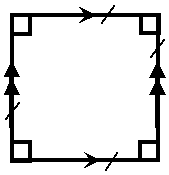
The square
A square is an even more specialised type of parallelogram than the rectangle. A square has all the properties of a rectangle, but on top of these, all the sides of a square are the same length:
The rhombus
A rhombus is like a square except that the interior angles can be any value at all, not just 90°. The square is a special type of rhombus.
|
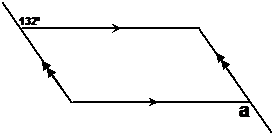
Find a:
|
|
Solution |
|
Sometimes these problems can be done quite quickly, if you keep an eye out for symmetrical or identical looking parts of the diagram. In this case, if you look more closely at the circled regions in the diagram, and extend a couple of the lines a little bit, you’ll see they’re identical:
Since these two areas are identical in their layout, all we need to do is find an appropriate rule that uses the 132° to work out what ‘a’ is. In this case, we have two straight lines crossing or intersecting each other. ‘a’ and the 132° are opposite each other, so they are opposite angles. We know that opposite angles are the same, so ‘a’ must be 132°. In this case we know that the two areas of the diagram are identical because the corresponding lines in each diagram are parallel to each other. For instance, line AB is parallel to line EF, and line CD is parallel to line GH. |
Closed shapes
A closed shape is one that doesn’t have any gaps in its border. A square or rectangle is a closed shape because you can start at a point on the border, and follow it around until you get back to where you started, without having to reverse direction. But if you had a shape which looked like a ‘C’, if you started at one point and kept moving, you’d have to eventually reverse direction to get back to where you started. It would not be a closed shape.
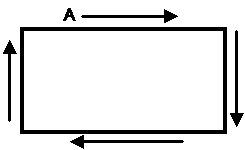
So a shape like this is a closed shape because you can always get back to where you started on the border, without having to reverse direction. You do change direction at the corners, which is OK, but you never have to stop and go back the way you came. But if you have a shape like this, you have to actually reverse direction: