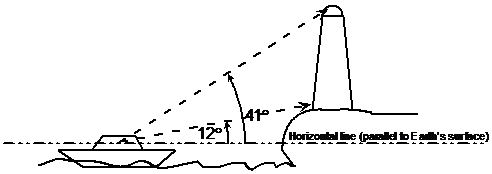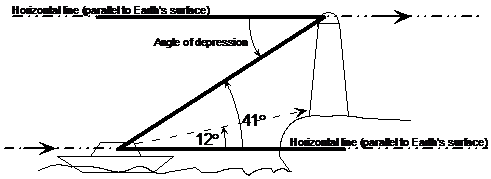There are lots of situations in everyday life where you need to look up or down at something a little distance away. For instance, if you are standing on the ground and looking at a bird in the top of a tree, chances are that you are looking in an upwards direction. But the opposite can also happen. Say you’re standing on the top floor of a building and looking out a window at the street next to the building. In this situation you are looking in a downwards direction.
In both of these situations you could also look straight ahead, so not upwards, not downwards, but in a horizontal direction. Usually horizontal in these cases means parallel to the surface of the Earth. When you look upwards or downwards, you can measure an angle relative to an imaginary horizontal line. If you look upwards, the angle relative to the horizontal line is called an angle of elevation. If you look downwards, the angle relative to the horizontal line is called an angle of depression.
Sponsored Links

In this diagram two people are standing on top of a building. The person on the left is looking upwards towards a car on top of a taller building. We can measure an angle of elevation from the horizontal to the direction he’s looking in. The person on the right is looking downwards at a car on the ground. We can measure an angle of depression from the horizontal to the direction he’s looking in.
|
For some reason, there are lots of questions involving boats and lighthouses when you talk about angles of elevation and depression. Here’s an example question: Bob is out in his boat for the weekend, when he catches sight of a lighthouse. He notices that the angle of elevation from his boat to the bottom of the lighthouse is 12°, and that the angle of elevation to the top of the lighthouse is a further 29° on top of this. Show this information on the diagram. The lighthouse keeper is at the top of his lighthouse and is looking at the boat. What type of angle is used to describe the direction he’s looking and how big is it?
|
|
Solution |
|
So we need to draw some angles of elevation into the diagram first. Remember that angles of elevation (or depression) are measured from the horizontal. Usually any line parallel to the surface of the Earth is horizontal. But what about when we’re on the ocean? Well, the ocean is pretty much flat, and is part of the Earth’s ‘surface’. So any line parallel to the ocean is horizontal too. Don’t worry about waves – just draw a line which is parallel to the overall direction of the ocean’s surface:
Now we need to draw in two angles of elevation – one to the bottom of the lighthouse, and one to the top. The angle to the bottom of the lighthouse is 12°. Be careful working out the angle to the top of the lighthouse – the question says it’s a further 29° on top of the 12° to the bottom. This means we have to add the two angles together to get the overall angle of elevation to the top of the lighthouse. This gives us 41°.
So now I’ve drawn in the two angles of elevation from the boat to the bottom and top of the lighthouse. The next part of the question talks about the lighthouse keeper who’s in the top of the lighthouse, and looking towards the boat. He’s obviously looking downwards, so this means it’s going to be an angle of depression. But how big is the angle going to be? We can use some of our knowledge from working with parallel lines to help here. By drawing another horizontal line at the level of the top of the lighthouse, we can create a ‘Z’ shape between two parallel lines.
To show the two horizontal lines are parallel, I’ve drawn an arrow along each one (check out the parallel lines section). Now, when we get a ‘Z’ between the two parallel lines, we know that certain angles are the same. We’re trying to find out what the angle of depression is. It’s an angle inside the top ‘corner’ of the ‘Z’. Our knowledge of parallel lines tells us that it is going to be the same size as the angle inside the other corner of the ‘Z’. This other angle is the 41°. So the angle of depression is 41°. Notice how the angle of elevation from the boat to the top of the lighthouse is the same value as the angle of depression from the top of the lighthouse to the boat. This is always the case when you swap between two viewing points. If you look from point A to point B and see an angle of elevation, then looking from point B to point A I’d see an angle of depression the same size. If you look from point A to point B and see an angle of depression, then looking from point B to point A I’d see an angle of elevation the same size. |
Handy Hint #1 - Making angles clear in diagrams
When you’ve got multiple angles close to each other in a diagram, make sure you make it clear which angle is which and what exactly are the angles between them. In the lighthouse diagram I’ve used arrows to show where the angles start and go to. Also, for the 41° angle, I’ve drawn the angle between the two triangle parts so that it’s clear that the 41° is measured all the way from the horizontal line to the top line. Two bad ways to draw this would be like this:

In this diagram the reader would probably think that the 41° angle was between the two direction of sight lines, instead of being between the horizontal line and the top direction of sight line.

This really isn’t much better. Now the reader isn’t sure whether the 41° is the angle between the two line of sight lines, or whether it’s the total angle. They may think
that the angle of elevation to the top line is actually the sum of the two angles –12° + 41° = 53°.

Drawing the angles this way makes it less confusing. The 12° is clearly measuring the angle between the horizontal line and the line of sight to the bottom of the lighthouse. It’s between the two lines, as well as being next to a curved arrow drawn pointing between the lines. The 41° is also clearly the angle from the horizontal line to the line of sight to the top of the lighthouse. By drawing it on top of the line of sight to the bottom of the lighthouse, the reader isn’t going to accidentally think it’s measuring either of the two smaller angles.