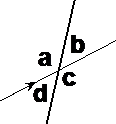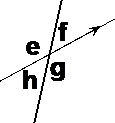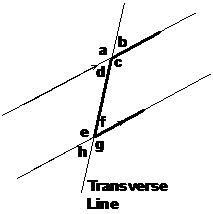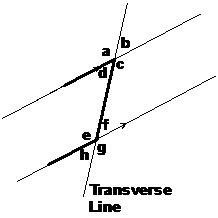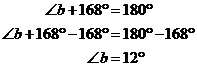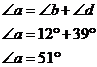You may already have a rough idea of what the word parallel means.  Note how it is spelt – with two ‘l’s in the middle but only one ‘l’ at the end.  You may have heard about parallel parking, or the parallel bars in gymnastics.  In mathematics, the word is usually applied to describe a certain arrangement of lines. 

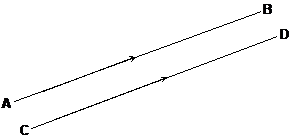
Look at the two lines in the diagram.  They are both straight lines – they are not curved.  Also, if we were to extend both lines – keep drawing along them in both directions to make them longer, they would never cross each other.  These two characteristics mean that these two lines are parallel.

Parallel lines are straight lines that never cross each other, no matter how long you draw them.

Here are a couple of examples of lines that are not parallel:

These two lines aren’t parallel because if you extend them, they eventually cross over each other.  The dotted lines show where these two lines have been extended.

These two lines aren’t classified as parallel lines because they are not straight. 

You need a way of showing in a diagram that two lines are parallel.  This can be done by drawing an arrow somewhere on all the lines that are parallel.  If there is more than one set of parallel lines, you can use different arrow types for each set, like in the following diagram:

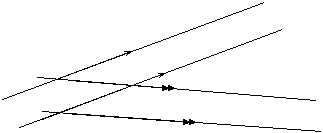
Here I’ve used a single arrowhead for one set of parallel lines.  For the other set of parallel lines I’ve used double arrowheads.

Transversal lines

Transversal lines are straight lines that cross over or intersect with two or more parallel lines.  There are all sorts of neat things that happen with the angles formed by a transversal line.

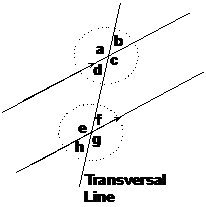
In this diagram there are two parallel lines and a transversal line.  There are also 8 angles where the transversal line cuts across the parallel lines – angles a, b, c, d, e, f, g, and h.

Corresponding angles

One of the neat things about transversal lines is that the areas where they intersect each parallel line all look the same.  This diagram shows the two circled regions and how they are exactly the same in their layout:

The top intersection	The bottom intersection

And this is where we get the idea of corresponding angles.  Look at angle ‘a’ and angle ‘e’ – they look like they could be the same size.  In fact, they are actually exactly the same size.  In mathematical terms, they are called corresponding angles.  The same applies for angles ‘b’ and ‘f’.  Since the two intersections are exactly the same, and since ‘b’ and ‘f’ are in the same part of the intersection, they are also known as corresponding angles, and are equal.  Same goes for ‘c’ and ‘g’, and also for ‘d’ and ‘h’. 

Alternate angles

Corresponding angles are not the only types of angles you can find when you have a transversal line cutting across two or more parallel lines.  There are also alternate angles, and there are two types of these as well.  If we go back to our diagram:

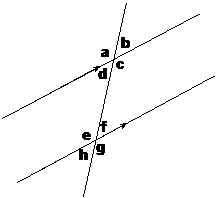
Interior alternate angles can be found by looking for the letter Z in the diagram:

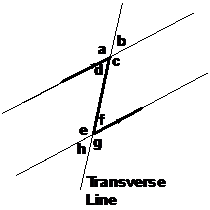
There are two sets of interior alternate angles.  One set is inside the corners of the Z.  In this case these are the angles ‘d’ and ‘f’.  The other set of interior alternate angles are the remaining angles that are between the two parallel lines – in this case angles ‘e’ and ‘c’.  This is why they are called interior alternate angles – because they are all between the two parallel lines.

External alternate angles can be found by looking for the letter ‘C’, either forwards or backwards:

Forwards ‘C’	Backwards ‘C’

The exterior alternate angles are found by looking above the top and below the bottom of the ‘C’.  For the forwards ‘C’, ‘b’ is above the top and ‘g’ is below the bottom, so these are exterior alternate angles.  For the backwards ‘C’, ‘a’ is above the top and ‘h’ is below the bottom, so ‘a’ and ‘h’ are exterior alternate angles.  The exterior part of the name means that these angles are outside the two parallel lines (i.e. not in-between them).

It’s also important to note that there are a lot of opposite angles in diagrams like these.  Remember that opposite angles are equal.  Here are the opposite angles for this diagram:

·         a and c

·         b and d

·         e and g

·         f and h

Co-interior angles

The two angles inside the ‘C’ are supplementary angles – they add up to 180°.  For the forwards ‘C’, the two angles inside it are ‘c’ and ‘f’, so we know that they add up to give 180°.  For the backwards ‘C’ the two angles inside it are ‘d’ and ‘e’ – so we know that these add up to 180° too.  These pairs of angles are called co-interior angles.  Mathematically we can write something like:

                                                    

So what’s the big deal with alternate angles?  Well, for the way we’ve paired them up, interior alternate angles are equal, and exterior alternate angles are supplementary.  So for the four sets of alternate angles we just found we can write some statements:

For the interior alternate angles:

                                                          

For the exterior alternate angles:

                                                    

Parallel lines question

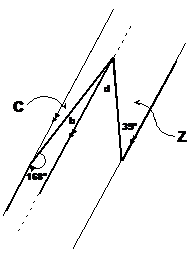
Find the value of a:

Solution

Okay, first time I ever looked at this problem, I had no idea how to do it.  Then, as I did more and more geometry questions, I learnt a few tricks and found a way to do it.  Whenever you’re stuck in geometry, one of the tricks which will most often get you out of trouble is to try adding lines to the diagram.  Sometimes by adding a line you’ll see a way to solve the problem.  Unfortunately, knowing where to add a line is something you can only learn through practise and experience, so do your homework!  But, back to this problem. In general, what you’re looking for is to add lines that will allow you to use a rule to solve the problem.  In this problem, angle ‘a’ doesn’t fit into any of the rules we’ve learnt for parallel lines.  There are no ‘C’s or ‘Z’s we can draw between the parallel lines either that will work.  So how about we try and add a line that will allow us to draw a ‘C’ or a ‘Z’?  One way we can do this is by adding another parallel line like this: Now, angle ‘a’ has been split up into two separate angles – which I have named ‘b’ and ‘d’ (I haven’t used ‘c’ as an angle so we don’t get confused with the ‘C’ shape we find in the next diagram).  We can remember that ‘a’ is made up of ‘b’ and ‘d’ by writing:                                                       So now we have a new problem to solve – if we can work out what  and  are, we will be able to calculate what  is. In our new diagram, we can now draw some ‘C’s and ‘Z’s, like this: Angle ‘b’ and the 168° angle are inside a very flat ‘C’, so we know that they are co-interior or supplementary angles and must add up to 180°:                                           Angle ‘d’ and the 39° are interior alternate angles, so we know that they are the same value.  This means that:                                                           Now that we know what  and  are, we can work out our final answer: