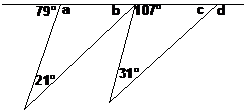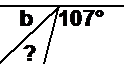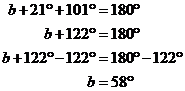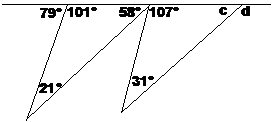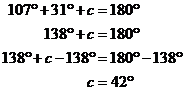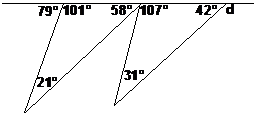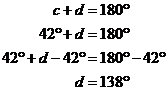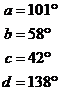Say you have a drawing of a triangle like this:
Sponsored Links
What happens if we extend one of the sides outwards a little, like this:
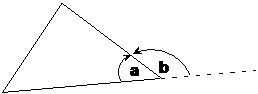
The dotted line shows where I have extended the bottom side of the triangle. Now we have two angles at the right corner – an interior angle ‘a’, and an exterior angle ‘b’. Interior means inside, and exterior means outside. One thing you can see straight away is that together these two angles make up a straight angle, or 180° in other words. This is true whenever you extend out a side of a triangle. The sum of the interior and exterior angles at the extension point is always 180°.
|
Find the values of a, b, c and d in the following diagram:
|
|
Solution |
|
Well, the first thing to do is have a look at the diagram. You can straightaway say a few things about it: · There’s a straight, horizontal line at the top of the diagram. · There are two triangles hanging off the bottom of this horizontal line. · There are 4 unknown angles and 4 known angles in the diagram. It’s important to have a general look at the diagram first, because it gives you an overall idea of what you need to do. For instance, by looking at the diagram I’ve reinforced in my mind that there are four unknown angles, like it says in the question. This means I’d better be sure my answer contains values for all four unknown angles. Now you can concentrate on trying to find out the values of the unknown angles. It’s best to start with the easiest ones and work your way up to the harder ones. Compare angle ‘a’ and angle ‘b’ for instance: · Angle ‘a’ can be found pretty quickly because it and the 79° angle make up a straight angle, or 180° in other words. It’s an easy angle to find. · Angle ‘b’ can be calculated in two different ways. We know that the sum of the interior angles of a triangle is 180°, so if we know the other two angles in the triangle we could work out ‘b’. Unfortunately, we currently only know one other interior angle – the 21°. The other way to work out ‘b’ is by noticing that it and the 107° angle form part of a straight angle, which we know is 180°. However, the third ‘part’ of this straight angle is also an unknown angle, so we can’t use that either.
So this shows how some angles are easier to work out at the beginning than others. In this case, we’ll start with working out what ‘a’ is: ‘a’ and the 79° angle together form a straight angle, or 180°. So we can write down something like: Take away 79° from both sides: Bingo – that’s one answer. We can re-label our diagram with this new information:
Let’s look at the situation again. Angle ‘b’ is now a lot easier to find – we now know both the other interior angles in the triangle - 21° and 101°. So we can write a mathematical equation showing how all the interior angles add up to 180°: After simplifying the equation, you get an answer out – b is 58°. We can again redraw the diagram with this new information:
So now we’ve only got ‘c’ and ‘d’ left to work out. Which one is the easier one to work out first? Well, ‘c’ is the interior angle of a triangle, and we know the other two angles in the triangle. The only useful rule we can use on ‘d’ is that together with ‘c’ it forms a straight angle, which is 180°. This isn’t much use however – we don’t know what ‘c’ is yet. So clearly, we need to work out what ‘c’ is first. Since we know the interior angles of a triangle add up to 180°, we can write something like this: And now we have a value for ‘c’. We can redraw the diagram again (once you get good at doing this you can skip redrawing the diagram every single time, which gets really repetitive).
All we have left to do is work out what ‘d’ is. This is easy – we have already seen that together ‘c’ and ‘d’ make up a straight angle – which is 180°. So we can write one last equation:
And there’s the last angle we had to work out. You may want to provide a summary at the end of your solution giving all the angle values, something like: |