The most common shape that you work with in geometry is the triangle. A triangle has three corner points and three straight sides, and must have an area. 3 points in a straight line do not form a triangle:
![]()
Sponsored Links
A triangle has to have some area – the line just shown has no area. If you make sure that the points do not form a straight line, you will get a shape with area – a triangle:
Types of triangles
Like angles, there are different types of triangles. You can describe types of triangles in two different ways. The first way is to look at the size of the interior angles in the triangle and describe it using them. The other way of describing triangles is to talk about them by looking at the sides of the triangle. Here I’ll go through all the different types of triangles, either described using angles or using sides.
Handy Hint #1 - Angles within a triangle rule
If you add up the three interior angles inside any triangle, they always add up to 180 degrees:
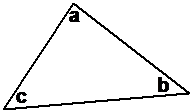
This means that for any triangle, such as the one shown above, the following rule is true:
![]()
Say you were given a triangle like the following one and asked to find what ‘a’ was:
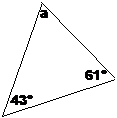
All you have to remember is that the sum of all the interior angles of a triangle is 180°. So you could write down a simple mathematical equation:
![]()
To work out what ‘a’ is you just need to simplify the equation and then work out what value of ‘a’ makes it true.
![]()
Subtract 104° from both sides:
![]()
And there you have your answer – a is 76°.

