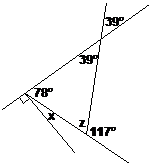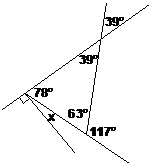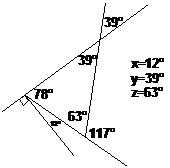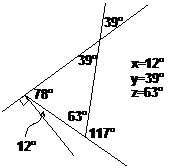So where does all this stuff come in useful? Well, a common question in tests that you might get would be something like:
|
Sponsored Links |
|
Solve for all the angles labelled in the diagram.
|
|
Solution |
|
Well, we’ve got to work out what x, y, and z are. To do this, we need to use some of the stuff we’ve just learnt on complementary, supplementary, vertically opposite angles etc… It’s usually best to start with what looks easiest in the diagram. In this case, working out what ‘y’ is looks like it will be the easiest – the ‘y’ and the 39° are vertically opposite angles, which means they are the same – so we know that ‘y’ is 39°. We can redraw the diagram with this extra piece of information:
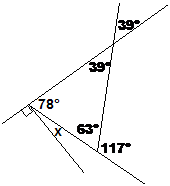
Now we’ve only got to solve what x and z are. Out of these, z looks the easiest to solve – z and the 117° together make up a straight angle, or 180 degrees in other words. In mathematical form we can write something like: Now you just have to work out what value of z makes this equation true. After a bit of thinking you should be able to work out that:
We redraw the diagram with that extra piece of information. That leaves us with one angle left to find – x. Now there are three angles in this area of the diagram – a right angle, x and also 78°. Together these angles make up a straight angle, or 180 degrees in other words.
So since these three angles together make up 180°, we can write down an equation: Now we know how many degrees there are in a right and a straight angle: In the left hand side of the equation, we can add the 90° and the 78° together: Now we just need to find a value of x that makes the equation true. After a little bit of thinking you should be able to get that: So we can work out that x is 12°. Finally, we can redraw the diagram one last time, with all the angles written in, and also give a summary of what each angle is:
Sometimes for very small angles (like x), you’ll need to write the angle in small letters to make it fit properly. One other way you can show the angle is like this:
|