There are quite a few different types of angles that you need to know. Learning these special types of angles is helpful because they help you use tricks that can make your life much easier when you’re doing calculations. If you know what type of angle you’re looking at you’ll be able to work out which trick to use to make your job easier.
Acute angles
Angles that are smaller than 90°. The ‘smaller than’ part is important – 90 degrees itself is not an acute angle.
Sponsored Links
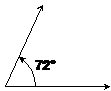
Right angles
90 degree angles get their own special name – they are known as right angles. They also get their own special angle symbol – instead of drawing a curved line to indicate the angle, you draw a little box like this:

Obtuse angles
Ok, so the names sound rather strange, but since they’re what everyone uses you have to learn them. Obtuse angles are between 90° and 180°.
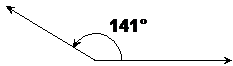
Straight angles
There’s a special name for angles which are exactly 180°. They are called straight angles. For once, the name makes perfect sense – when you draw this angle you draw a straight line!
![]()
Reflex angles
Well, that only leaves us with the angles between 180 and 360 degrees. These angles are called reflex angles.

360 degrees
An angle which is 360 degrees is often called a revolution. One of the very important things to know about an angle that is 360 degrees is that it is the same as an angle of 0 degrees. This is because when you rotate through 360 degrees, you end up back where you started – which is at 0 degrees:
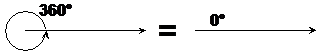
This rule also applies for angles larger than 360°. For instance, say I rotated around 372°. This is the same angle as 12 degrees, as can be seen:
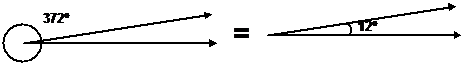
An easy way to simplify any angle over 360 degrees is to keep taking away 360 from it until the angle is between 0 and 360 degrees. For instance, if I got given 800 degrees, I would do this:
![]()
440° is larger than 360° so I need to keep subtracting 360 from it:
![]()
Bingo – an 800° angle is the same as 80° angle.
When not to simplify angles larger than 360 degrees
In some situations, angles larger than 360 degrees can be meaningful. For instance, say you’re watching a car race on television and a car loses control and spins completely around twice. If you were describing this to someone later, you might say something like, “The car lost control and spun 720 degrees.” By saying 720 degrees, you are telling the person that the car did two complete spins – since one complete revolution or spin is 360 degrees.
Skateboarders, snowboarders, wake boarders, surfers, skiers and many other extreme sports people often use terms like this to describe special tricks they do. A simple trick on a surfboard is called a ‘360’, whereby whilst riding a wave the surfer spins the board through 360 degrees – hence the name ‘360’.
Complementary angles
When someone talks about complementary angles they are talking about not one, but two angles. Complementary angles add up to 90°. 50° and 40° are complementary angles for instance. Since complementary angles add up to 90°, you know that none of them can be 90° or larger. Complementary angles are usually easy to spot because put together they make a right angle. Look at this diagram for instance:
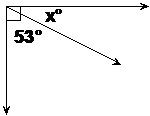
First thing to notice is that there are three angles in the diagram. There is a 53° angle, an ‘x°’ angle, and a right angle. Also notice that for the 53° and the x° I haven’t bothered to draw in a curved line showing the angle – for such a simple diagram it’s pretty clear what each angle corresponds to.
Say I had to work out what ‘x’ was equal to. Now, like in an exam, to work out the answer, you probably need to use something that you’ve just recently learnt. We’ve just been talking about complementary angles, so what about trying to use this to our advantage. Looking at the diagram, you can see that the right angle is made up of the 53° and the x°. In other words:
![]()
We have to think of an angle that when added to 53° gives us 90°. This isn’t too hard, if you think about it for a bit you should get that:
![]()
This means that x is 37.
Supplementary angles
These are very similar to complementary angles, except that they have to add up to 180°, not 90°. So for example, 60° and 120° are supplementary angles. Another way of saying this would be “120 degrees is the supplement of 60 degrees.”
Supplementary angles are easy to spot in diagrams because they make up a straight angle. Here’s a diagram showing two supplementary angles:
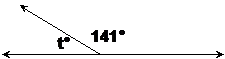
In this diagram, t° and 141° are supplementary angles, since together they make up a straight angle, or 180 degrees in other words. If we wrote this down in a mathematical way it would look like this:
![]()
This is easy to solve – we just have to work out the value of ‘t’ that would make this equation true. If you think about it for a while you should get:
![]()
and work out that t is 39.
Vertically opposite angles
Say I draw two straight lines that intersect, and label the four angles that are formed:
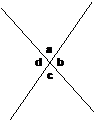
Notice how each angle has an angle opposite it – for instance, ‘a’ has ‘c’ opposite it, and ‘d’ has ‘b’ opposite it. These two pairs of angles are known as vertically opposite angles. Vertically opposite angles are equal in value – so in this diagram ‘a’ is the same size as ‘c’, and ‘d’ is the same as ‘b’. This is very useful when you have situations like this:

Since ‘a’ and the 121° are vertically opposite, you can immediately work out that ‘a’ is 121° as well.
Describing angles
Any angle is measured between two different directions. Usually in a diagram, these directions are shown as lines, sometimes with arrows on them. In an exam, you may come across a diagram like this:

You can see that there’s an angle formed between these two lines – I’ve shown it by drawing in a curved line. But how do you describe this angle in a proper mathematical way? Well, that’s where you can use the labels A, B and C in the diagram. To describe this angle, you first need to write down the labels at the ends of the two lines the angle is between, with a gap in-between them like this:
A C
The gap you left is for the label at the point where the angle actually is. In this case, the angle is at point B, so we fill the gap with a ‘B’:
ABC
Now, to make sure that everyone knows we’re talking about an angle, rather than just a sequence of letters, we use a special angle symbol and put it before the letters:
![]()
This means, “the angle at point B, which is between the lines pointing from B towards point A and point C.”

