Symmetry is all about having parts that are reflections of each other. For instance, a simple square is symmetrical in several ways.
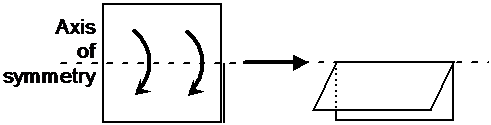
Sponsored Links
You can take a square sheet of paper and fold it over to create a rectangle like in the diagram. If you fold it so the edges all meet up exactly, the line you folded over is called the axis of symmetry. There are two ways you can think about an axis of symmetry. One is this way – if you can fold a shape over so that one half exactly overlaps the other half, you have folded along the axis of symmetry.
The other way is to think about reflections in a mirror. If you placed a mirror along an axis of symmetry, then everything on one side of the mirror would be ‘reflected’ to the other side like this:
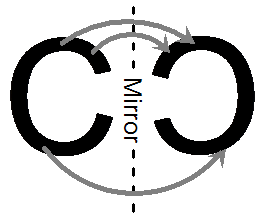
In this picture, on the left hand side of the ‘mirror’ there is the letter ‘C’. On the right hand side of the mirror is its ‘reflection’. Notice how the ‘direction’ of the ‘C’ swaps when it is reflected – on one side it faces forwards, on the other it is back to front. Also notice how parts of the shape that are close to the mirror are also close to the mirror in the reflection. But parts that are far away from the mirror on one side are also far away on the other side. You get to choose whether you prefer the folding or mirror way of thinking about symmetry.
Multiple axes of symmetry
Some shapes aren’t symmetrical at all. Others have an axis of symmetry. Some special shapes have more than one axis of symmetry. The plural form of axis is ‘axes’. So what are some shapes that have more than one axis of symmetry? Well, one very well known shape is the square. Look at all its axes of symmetry:
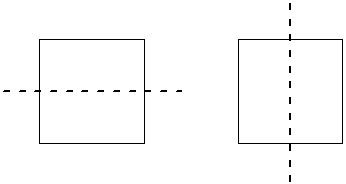
It’s got horizontal and vertical axes of symmetry:
But that’s not all! It also has two diagonal axes of symmetry. Remember, these axes can be at any angle:
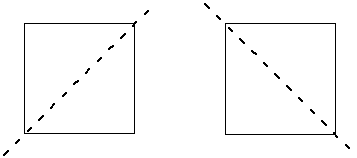
So all up, a square has four axes of symmetry.
Symmetry and letters
Usually when you’re doing symmetry and mirror images, you get to work with letters. It’s good to know which letters have axes of symmetry, how many axes they have, and also the letters which have or display no symmetry. You’ve got to be a little bit careful too, take the letter ‘o’ for instance. Now, if you draw your ‘o’s as an ellipse then it’s only got two axes of symmetry:

But what about if you draw your ‘o’s as a circle. Then, you can draw any number of axes of symmetry. Basically, any line through the centre of the circle is an axis of symmetry:
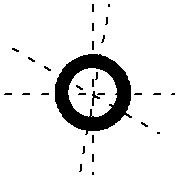
So for a circular ‘o’, there are infinite axes of symmetry.
Reflecting using x- and y-axes
Some questions will show you a shape on a set of x- and y-axes, and ask you to reflect it across one of the axes. For instance, say you had to reflect this triangle across the x-axis:
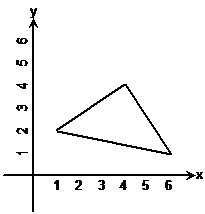
For a shape like this, you have to work out what the coordinates of the corners are. You can do this by looking at where each corner lines up with the axes. Once you’ve worked out the coordinates, you can label each corner:
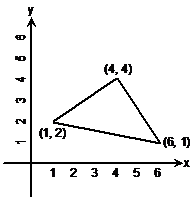
Now, we’re reflecting this shape across the x-axis. We can already roughly draw in some arrows showing where we think each corner’s going to end up:
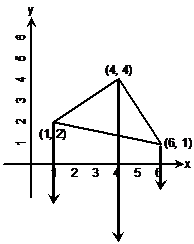
Now look carefully at the arrows showing where the points are going to move to. Notice how they travel straight down. When you travel straight down, the ‘y’ value of your location changes. In this case, as you go downwards, the ‘y’ value decreases. Take the left corner for instance. You start at a y value of 2, but as you go downwards, this value decreases to 1, then 0, and then you start going negative… –1, –2 etc…
But what doesn’t change is the value of x. If you move straight down, your x value stays the same. For the left corner as you move downwards, your x value is always 1.
So to reflect our triangle across the x-axis, all we have to do is work out how far above the x-axis each corner is, and put the reflection of that point that far below the x-axis.
For the left corner – its y value is ‘2’. So to
reflect it we need to put a point 2 units below the x-axis, or in other words,
with a ‘–2’ value of y. Its x value will be the same however, at ![]() . For the top
corner, it’s 4 above the x-axis, so we need to put its reflection 4 below the
x-axis, at y = –4. And for the right corner, it’s only 1 above the x-axis, so
we need to put its reflection 1 below the x-axis, at y = –1. Its x value stays
the same as well, at
. For the top
corner, it’s 4 above the x-axis, so we need to put its reflection 4 below the
x-axis, at y = –4. And for the right corner, it’s only 1 above the x-axis, so
we need to put its reflection 1 below the x-axis, at y = –1. Its x value stays
the same as well, at ![]() .
.
So your reflected shape should look like:
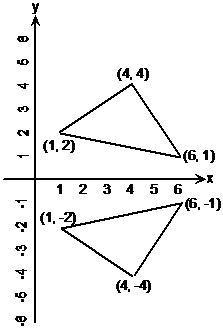
Now if you had to reflect a shape across the y-axis, then you’d have to do the reverse of what you did here. So instead of moving the corners in a vertical direction, you’d be moving them sideways. When you move sideways, your x value changes but your y value stays the same. So for instance, if we reflected the (1, 2) corner in our original shape across the y-axis, the y value would stay the same, but the x value would become negative. So it would change to a point at (–1, 2). The whole shape reflected across the y-axis would look like:
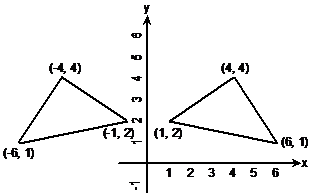
Important things to notice for this second reflection is that the x values have all become negative, but the y values have stayed the same.
Sometimes you’ll be asked to perform more than one mirror image or reflection on the same shape. So you might have to reflect a shape across the x-axis, and then reflect that reflection across the y-axis. With practice you can do these problems quickly and easily. Also, after a while you’ll be able to tell pretty quickly whether your answer looks ‘right’.

