Asymptote plotting question

Sketch the following function:

Solution

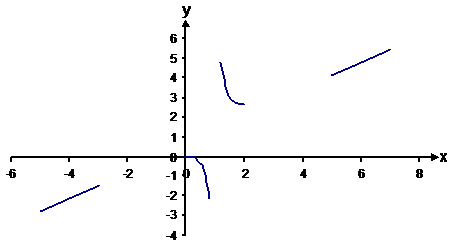
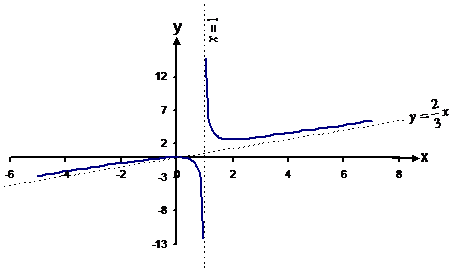
The function is undefined at x = 1 – the denominator equals 0.

First, we see how the function behaves as we approach the four points:

Approaching :

The function becomes  for large negative values of x, since you can ignore the ‘’. This simplifies to .

Approaching  from the negative side:

The function approaches a very large negative number. For x values just below 1, the numerator is positive and the denominator is a very small negative number.

Approaching   from the positive side:

The function approaches a very large positive number. For x values just above 1, the numerator is positive and the denominator is a very small positive number.

Approaching :

The function becomes  for large positive values of x, since you can ignore the ‘’. This simplifies to .

So at both large negative and large positive values of x, the function is very close to a straight line described by the function .  So you can draw an asymptote . Near large negative and positive values of x, the function follows this asymptote. There is also a vertical asymptote at x = 1, where the function is undefined.  You can draw what the function looks like near this as well.

The next thing to check for is x-axis and y-axis intercepts:

·         y-axis intercepts happen when x = 0 – there is a y-axis intercept at y = 0.

·         x-axis intercepts happen when y = 0 – there is an x-axis intercept at x = 0.

We can sketch this preliminary information on a graph:

The graph passes through the origin. From looking at the sketch so far, it looks like the left-hand side of the graph will be what passes through the origin. Now all you do is connect up the lines, remembering the intercept through the origin. You can also draw the two asymptotes in as straight dotted lines:

Some notes

The first function sketched in this section was a fairly easy, standard sort of asymptote graph.  The function we just sketched for this question is an example of a more complicated sort of graph.  For example, the right hand part of the curve does not cross the  asymptote, but the left-hand part does.

The only way to tell that this happens is to use the axis intercept information – we found that the left hand part of the curve crossed through the origin.  So we drew the curve through the origin, and then brought it back towards the  asymptote, because we knew that towards , the function approaches the straight line function .