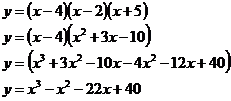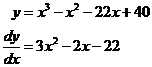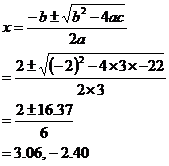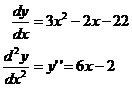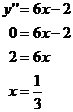If you are given a function to sketch, you must include several pieces of information on the sketch.
Let’s illustrate the typical process taken to sketch a function.
Sponsored Links
|
Sketch the function |
|
Solution |
|
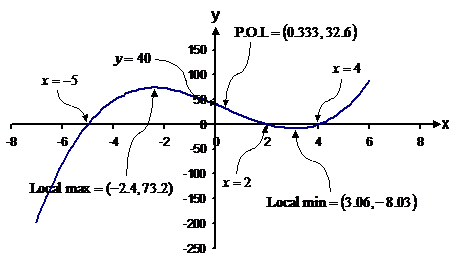
To find x-axis intercepts, you set y = 0. Note that there are not always x-axis intercepts. The function is in an easy form to calculate the x-axis intercepts – you set: For this to be true, one of the bracketed terms must be 0. If the first bracket = 0, x = 4. If the second bracket = 0, x = 2. If the third bracket = 0, x = –5. So the x-axis intercepts are at x = –5, 2, and 4. If the function is not in such a convenient form you may have to use the quadratic formula, or polynomial division to work out x-axis intercepts. To find the y-axis intercept, you just set x = 0, and evaluate what y is. Remember there is only one y-axis intercept. So the function crosses the y-axis at y = 40. These are places where the function has a ‘hill’ or a ‘valley’. Local maxima are hills, and local minima are valleys. Maxima is the plural form of maximum, and minima is the plural form of minimum. To find them, use the fact that the bottom of a valley or the top of a hill is a horizontal line. A horizontal line has a slope of 0. The derivative of a function at a point finds the slope of the function at that point. So if we set the derivative of this function to equal 0, then we can find where the local maxima and minima occur. First, we must find the derivative – let’s multiply out the brackets. We multiply the brackets out because it is easier to find the derivative that way, rather than using the product rule on the function in its original form. Now differentiate it: Now we set the derivative to = 0, and solve for x. Use the quadratic formula, since it doesn’t factorise easily: Another name for a local maximum or minimum is a turning point. There is one problem with these x-values – we don’t know whether they specify the position of local maxima or minima (hills or valleys). We can use something called the second derivative to find out which type they are. The second derivative just means differentiating our first derivative again. Our first
derivative is If we differentiate it, we get: where Now all we do is substitute the x-values of our turning points into the second derivative. If the result is positive, it is a local minimum (valley), if it is negative, it is a local maximum (hill). For x = 3.06: This is a positive number, so it means there is a
local minimum at x = 3.06. The actual value 16.36 doesn’t matter, all that
matters is that it is positive. We calculate the y-value of the turning
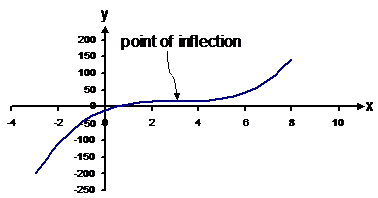
point by substituting x = 3.06 into the original function, to get For x = –2.4: This is a negative number, so it means there is a local maximum at x = –2.4. The y-value of the turning point is 73.2. Points of horizontal inflection A point of horizontal inflection is a point where the gradient/slope of the function is 0, and the slope immediately on either side of the point is of the same sign. Either the slope on both sides is positive or the slope on both sides is negative. In general, a point of horizontal inflection occurs where the first derivative of the function is 0, and the second derivative of the function is 0. For the function we are sketching, the double derivative is not 0 at both places where the first derivative is 0. Therefore there are no points of horizontal inflection in this function. Here is an example of a horizontal point of inflection:
Now back to the function we are sketching: Points of inflection occur wherever the second derivative of a function is 0. Unlike horizontal points of inflection, they do not require the first derivative to equal 0. A horizontal point of inflection is a special case of the more general point of inflection. So we set the double derivative/second derivative to = 0, to find where our points of inflection occur: So there is point of inflection at Another way of finding points of inflection, is that they occur when a function switches from concave upwards to concave downwards, or vice-versa.
Here are two examples:
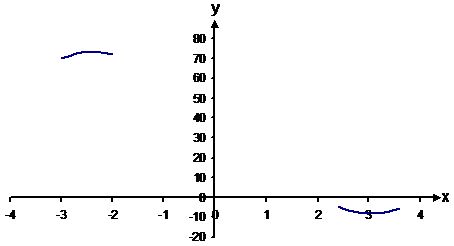
Stationary points are anywhere on the function which has a first derivative equal to 0. They can be local maxima, minima, or points of horizontal inflection (but not general points of inflection). Critical points are anywhere on the function where the first derivative is 0 or where the first derivative does not exist and the function is defined. Our first derivative function is So now we can go about sketching our function. First of all, at the turning points, draw little hills or valleys, depending on whether they are maxima or minima:
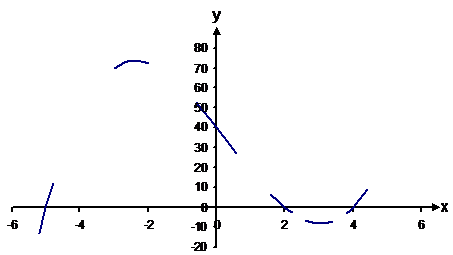
The next step is to draw where the lines cross the x-axis – at x = –5, 2, and 4, and the y-axis – at y = 40.
Then all the lines were just joined up.
Typically, you would label the x- and y-axis intercepts, the turning point coordinates, and the point of inflection. It is your choice how far to continue the graph to the left and right hand sides – just far enough to give an idea whether it is always increasing or decreasing is usually enough. |
If you have to use polynomial division to find the x-axis intercepts, leave this till last – it is very time consuming, and also difficult to do without making any mistakes. If you run out of time to calculate the x-axis intercepts, make some reasonable guesses where the line might cross the x-axis based on the shape of the function that you’ve already plotted, and the type of function (is it a linear, cubic etc. function)