Amplitude transformations

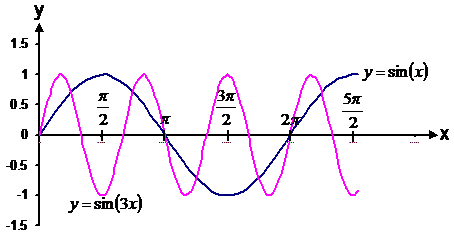
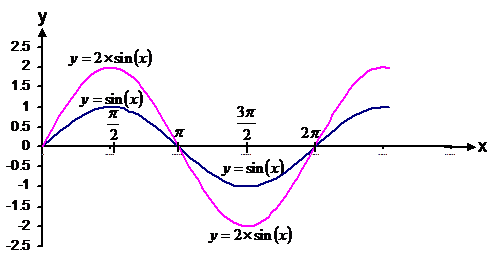
Say I have to graph the function . To get this graph, all you do is take the normal sin(x) graph, and stretch it in the vertical direction by a factor of 2.

If the number had been ‘–2’, you would stretch the graph in the vertical direction by a factor of 2, then take its mirror image about the x-axis.

Sideways movement

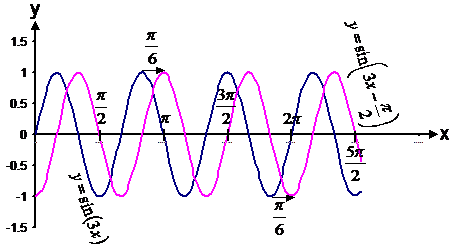
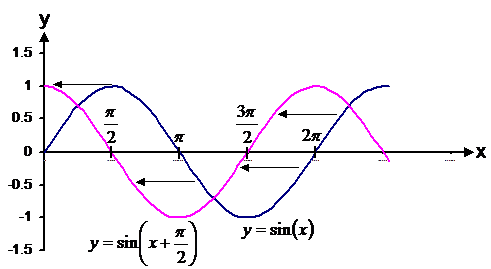
What about if I have to graph ?  If the sign in the brackets is positive, this shifts the graph to the left by whatever is to the right of the ‘+’ sign.  If the sign is negative, this shifts the graph to the right by whatever is to the right of the ‘–’ sign.  Since in this case, the sign is positive, it shifts the graph  to the left.      

Horizontal squashing or stretching

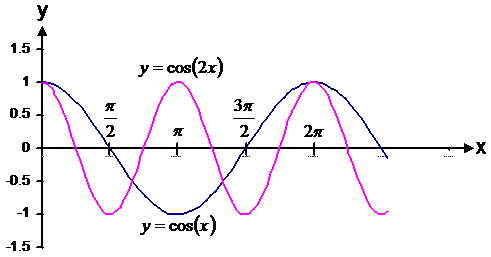
Another type of function you might have to plot is something like.  This time the 'x' has a coefficient in front of it.  When this coefficient is larger than 1 (as it is in this case), the graph is compressed sideways (horizontally).  If it is smaller than 1, the graph is stretched sideways.  In this case, since 2 is larger than 1, the graph is compressed sideways by a factor of 2.

 

Vertical displacements

For a function like , all you do is shift the entire  curve upwards by 2 units.

Sign changes

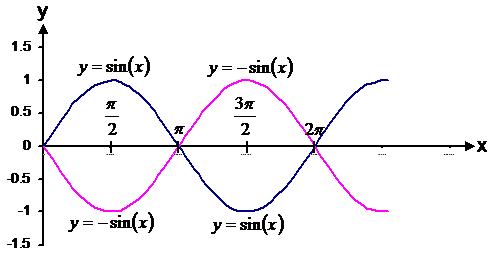
Say I want to draw the curve . The easy way to do this is to first draw the curve , then simply reflect it over the horizontal line of symmetry – the x-axis in this case. 

What about when the negative is actually inside the brackets?  An example of this would be .  For this curve, you need to remember that , so they are the same curve.  However, say you had to plot . For this you need to know that .  So to draw , you would first draw .  Then you would reflect it over the horizontal line of symmetry (usually the x-axis) to get .

Putting it all together

Often you will have to plot quite complex functions that involve sometimes all of these things.  Whenever you get a function to plot, you want to get it in the general form:

                                                 

                                               or

                                               or

Remember that ‘b’, ‘c’, and ‘d’ can be zero – the result is usually a simpler function.

Periodic graph plotting question

Plot the following function for :

Solution

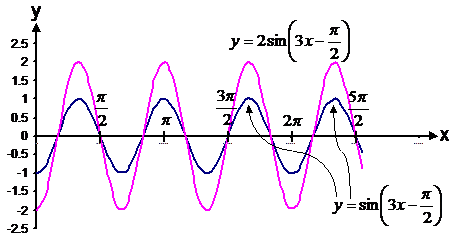
This equation is already in the general form that we desire.  Since it is a sin function, we first draw the simplest curve we know, .  Next we deal with the 3 in front of the ‘x’ – we now draw the next simplest function, .  This is simply the  curve squashed sideways a lot.  The next part to deal with is the  ‘’ part.  We can plot  simply by shifting the  graph to the right by . Why do we shift the graph by , not ?  This is because of the 3 in front of the ‘x’.  If it had just been  then we would have shifted the graph by  to the right.  But because there is a 3 in front of the ‘x’, we shift the graph by ‘ divided by 3’ – which is .   The next step is to allow for the 2 in front of the .  This is easy to do – we just stretch the graph vertically by a factor of 2.  Now the curve goes from –2 to 2 in the y direction, instead of –1 to 1 as it did previously. 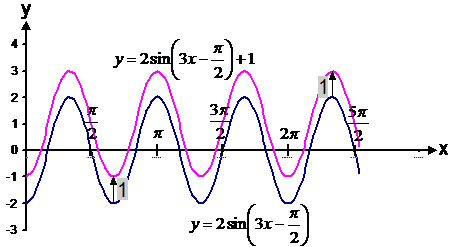The last step is to allow for the ‘+1’.  This is also very simple – we shift the curve up by 1 in the vertical direction.  So by using a step by step approach, you can break up a fairly hard problem into easy bits that by themselves are quite simple.