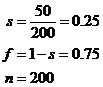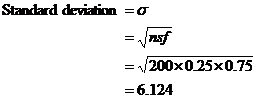When you have large sample sizes, you can’t look up tables. We use the approximation of the normal distribution instead to do our calculations.
|
Large sample confidence interval question Sponsored Links |
|
Say I have 200 school students at a school. 50 of them need lunch provided for them at school. If I have another identical group of 200 school students, find the 95% confidence interval in terms of how many will need lunch provided. |
|
Solution |
|
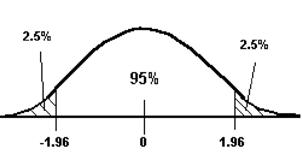
Now if I have a normal distribution curve, and I need a 95% confidence interval, it means that the middle area will be 95%. The two outer areas, one on each side of the middle area, will be 2.5%. Note how this is a two-sided question – we are interested in the small 2.5% probability areas on both sides of the central peak. Firstly, we must find how many standard deviations
from the middle the 2.5% areas are. They are
They are 1.96 standard deviations from the centre. Now: First, let’s check we can use the normal distribution approximation: For our sample, one standard deviation is: And so, 1.96 standard deviations = 1.96 ´ 6.124 = 12. · Lowest possible number of lunches needed = 50 – 12 = 38. · Highest possible number of lunches needed = 50 + 12 = 62. So, for the new 200 students, we could be 95% sure that at least 38 would need lunch, but no more than 62. |
from the centre, so we look up a
standard deviation table.
