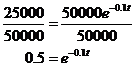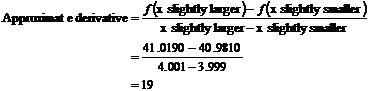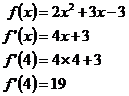Solving dy/dx=ky

There is a special type of function of the above form that has a special solution.  By solution, we mean the function y = … that is equivalent to it.

For the general function , where ‘k’ is a constant, the general solution is:

Sponsored Links

                                                          

where ‘A’ is another constant.

When you are given an actual problem with real numbers in it, you can calculate what A is equal to.  For instance:

Water flow question

The rate of water flow out of a hole in a pool is described by this expression:

                                                       

‘w’ is the amount of water left in the pool in litres.  The pool starts with 50,000 L.  How long will it take for the pool to half empty (‘t’ is in seconds).

Solution

The expression  fits the general function form shown above.  Therefore it must have the same general solution:

However, instead of ‘y’, we have ‘w’.

Instead of ‘x’ we have ‘t’.

So the general solution is .

Now, using the information given to us in the question, we can work out what A is.

At time t = 0 seconds, the pool has not yet lost any water, so it has 50,000 litres in it.  So we substitute this information into our general solution:

                                                 

                                

Anything to the power 0 is 1, so:

                                                     

The expression for water left in the pool is:

                                                       w = 50 000e-0.1t

The question was, how long before the pool is half full.  When it is half full, there are 25,000 litres in it.  So:

When it is half full, w = 25,000, we need to find ‘t’.

                                                                  

Divide both sides by 50000:

                                                 

You take the natural log of both sides (ln) to solve this for ‘t’:

                                                    

Remember, natural log is asking what power you must raise ‘e’ by to get ‘’. The answer is simple, it is just ‘–0.1t’. You can evaluate ‘’ using a calculator.

                                              

Obviously, this must be a very big hole!

Handy Hint #1 -  Approximate derivatives

Sometimes, when you can’t work out what the derivative of a function is, maybe because it is too complicated, you can use approximate derivatives. The derivative of a function represents the rate of change of that function.  The derivative at a particular point is the rate of change at that point. The following question shows how you can work out an approximate derivative.

Approximate derivative question

Work out the approximate derivative of this function at x = 4:

                                                        

Solution

To work out the approximate derivative, take two ‘x’ points, one slightly above where you want to find derivative, one slightly below. Let’s use x = 3.999, and x = 4.001.

Work out what the function equals at these two points.

x = 3.999:

                                                 

x = 4.001:

                                                 

It is important that you write down a fair number of decimal places in your calculations, or even better, store the values in your calculator memory.

Then, substitute into this expression:

                   

Let’s check this with the exact derivative:

                                                 

This technique will not always work, so don’t rely on it, but you can use it to check your answers, or as a backup in case you can’t differentiate a function.  In general, the more complicated the function, the closer your larger and smaller ‘x’s should be to the actual ‘x’ – maybe use ±0.000001 instead of ±0.001.