The trapezoidal rule can be summarised as:

                                        

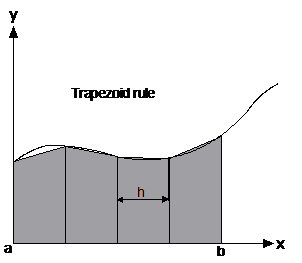
The trapezoidal rule involves representing the function as a number of trapezoids that fit underneath the curve. Note that it is often also called the ‘trapezoid rule’ with no ‘al’ at the end of ‘trapezoid’.

·         ‘h’ is the width of these trapezoids.

·         ‘E’ is f(a) + f(b):

·         ‘M’ is the sum of f(a + h) + f(a + 2h) + f(a + 3h) + … + f(b – h).

·         ‘a’ is the left-most x-coordinate, ‘b’ is the right-most x-coordinate.

Trapezoidal rule question

Find the area underneath the function  between x = 0 and x = 10.

Solution

Firstly decide how many trapezoids we want to use to approximate the function – let’s use 5.  Also, a = 0 and b = 10. If we use 5 trapezoids, then each one must be 2 units wide – since the total interval is 10 units. So h = 2.                                                                                          Now, substituting h, E and M into our formula:

If you have curves that are both under and above the x-axis, then you must work out their areas in ‘bits’ using these methods just like you have to for integration. This means you need to work out the area above the x-axis, then work out the area below the x-axis, and add the results together. The more rectangles or trapezoids you split your graph into, the more accurate your answer will be, but the longer it will take to calculate.