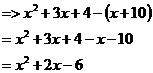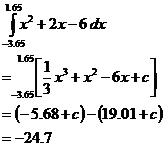Areas between curves question

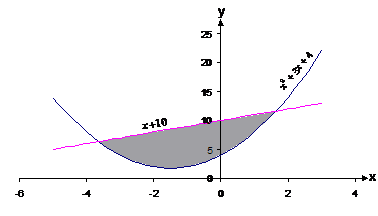
Find the area cut off the curve f(x) = x² + 3x + 4 by the straight line f(x) = x + 10.

Solution

Firstly need to sketch the two curves to get an idea of what we are trying to do.

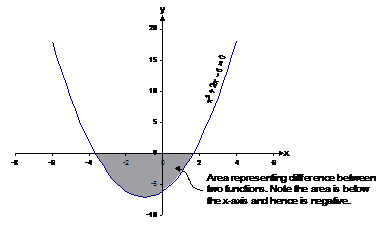
Now that the two curves have been drawn, we have a rough idea of the area that needs to be calculated.  From the graph it can be seen that it is going to be from about  to .

The difference function is just one function subtracted from the other – it doesn’t matter which order.

Let’s subtract (x+10) from (x² + 3x + 4):

We can plot this function on a graph. The y-value of the graph at any point represents the difference between the two functions at that point. You can see that the curve crosses the x-axis (and hence has a y value of zero) at two points in the new graph – these points represent where the two function lines cross over each other in the first graph.

We are only interested in the area between the two intersections of the two functions.  To find the x-coordinates of these intersections, we set each function to equal the other: 

Rearranging we get:

Using the quadratic formula, we can solve this to find that x = –3.65, 1.65.  Be careful with the quadratic equation however, as you can easily forget to cancel out negatives, or even include them.

Now all we have to do is find the definite integral of the difference function between these values:

You can take the absolute value of this answer, since we’re just interested in the amount of area, not whether it happens to be above or below the x-axis in our difference function.  It is negative only because of which function we chose to subtract from the other.  In general, just take the absolute value of your result for the answer. So the answer is:

These questions can get quite complicated if the functions intersect each other several times.