If a curve passes below the x-axis, if you use integration to find the area between the curve and the x-axis, it will give you a negative area. For instance, if I use integration to find the area between the curve in the previous section and the x-axis between x = 1 and x = 2, I would get a negative number.
This means if I want to find the total area between the curve and the x-axis between, say, x = –4 and x = 2, I must do it in two separate parts. If I don’t, the negative area will cancel out part of the positive area.
Sponsored Links
One part is when the curve is above the x-axis from x = –4 to x = –1. The other part is when the curve is below the x-axis, from x = –1 to 2.
First part (x = –4 to x = –1)
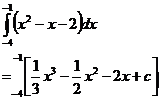
The square brackets are a short hand way of saying that we have already worked out the indefinite integral, which is written in between the square brackets. They indicate that all that is left to do is:
· Substitute the top number in the integral sign into the expression and evaluate it (top number is –1 in this case).
· Substitute the bottom number on the integral sign into the expression and evaluate it (bottom number is –4 in this case).
· Subtract the second result from the first one.
So substituting the top number in the integral sign
into the expression gives ![]() .
.
Substituting the bottom number in the integral sign
into the expression gives ![]() .
.
Subtracting the second result from the first gives (the
‘c’s cancel out) ![]() .
.
Second part (x = –1 to x = 2)
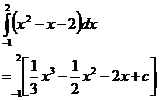
Substituting the top number in the integral sign into
the expression gives ![]() .
.
Substituting the bottom number in the integral sign
into the expression gives ![]() .
.
Subtracting the second result from the first gives ![]() .
.
Note how this is a negative result. The actual
physical area between the curve and the x-axis between x = –1 and x = 2 is just
the absolute value of this, ![]() .
.
To work out the total area between the curve and the x-axis between x = –4 and x = 2, just add the two areas together:
![]()
In general, if you need to work out the area between a curve and the x-axis, you must split it up into ‘positive’ areas and ‘negative’ areas and follow the process above. You can find where the curve crosses the x-axis by setting y = 0 in the function.

