Integration and differentiation both have uses in finding information about graphs of functions.  We already know that the derivative of a function gives the slope of the function.  The definite integral between two points gives the area between the function and the x-axis.

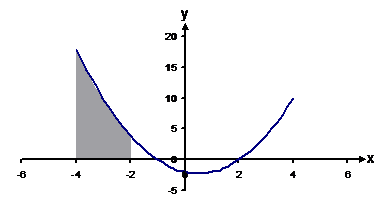
As an example, look at this graph of the function .  If I wanted to find the area between the curve and the x-axis (x-axis located at y = 0) between say x = –4 and x = –2, I would take the following definite integral:

                                                     

Note that the left-most point (x = –4) is put on the bottom of the integral sign, and the right-most point (x = –2) is put on the top.            

The indefinite integral is:

                                                  

I substitute the top number (–2) on the integral sign into this indefinite integral and get:

                                                           

Then I substitute the bottom number (–4) on the integral sign into the indefinite integral and get:

                                                          

I subtract the second result from the first:

                                             

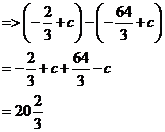
This is the area between the curve and the x-axis between x = –4 and x = –2.