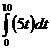One of the most common uses of differentiation and integration is when you are concerned with the motion of a body, such as a person or car.
There are three things that can describe a body’s position and movement; position, velocity and acceleration.
Sponsored Links
· Position is where the body is located.
· Velocity is how fast the body is moving, and in which direction.
· Acceleration is a measure of whether the body’s velocity is getting faster or slower, and how quickly (this is a simplified definition).
If you know one of these three things, you can obtain information about the other two using differentiation and integration.
· You can get velocity by differentiating the body’s position function.
· You can get acceleration by differentiating the body’s velocity function.
Likewise, you can use integration to go in reverse:
· You can get velocity by integrating the body’s acceleration function.
· You can get position by integrating the body’s velocity function.
Another way of visualising this is:
Differentiation: ![]()
Integration: ![]()
Let’s illustrate these principles with an example:
|
A truck starts moving down a road. The expression for its velocity is (5t) m/s, where t is the time in seconds since it started moving. After 10 seconds, how far has it moved from where it started? |
|
Solution |
|
If the truck was moving at a constant velocity, this problem would be easy to solve using simple maths. But its velocity gets larger and larger as time goes on. So we must use another technique. The question asks how far it has moved – which of the three (position, velocity and acceleration) are most directly related to distance? The truck’s position is most closely related to how far it has moved. We have an expression for the truck’s velocity, but we are interested in the truck’s position. So we need to get from velocity to position – we use integration. Now, do we need an indefinite integral or a definite integral? Well, we’re interested in how far the truck has moved between the start time and the end time. The problem states it wants to find how far the truck has gone after a specific time – we need a definite integral. What are the numbers to put in our definite integral? Well, we’re interested in how far the truck has moved between the start time and the end time. So the numbers to put in are the time when the truck starts moving, and the time at the end. It starts at time = 0 and finishes at time = 10. Now we can write the definite integral: Note how now it is a ‘dt’ at the end instead of a ‘dx’. In general, you write ‘d_’ and put whatever in the function is changing – in this case ‘t’, in previous cases it was ‘x’. So by integrating we can change the velocity function into a position function. Let’s work out what the position function is: Integrating we get: We now have an expression for the truck’s position after ‘t’ seconds. So now we work out what this expression equals for 10 seconds (the top number): Then we work out what this expression equals for 0 seconds (the bottom number): Then we subtract the second result from the first: Answer: The truck travels a total distance of 250 m in the 10 seconds. |