Integration

Integration can be thought of as the reverse of differentiation.  It is like doing differentiation in reverse.  Like differentiation, it has rules on how it should be done.

The constant of integration

Whenever you integrate something, you always have something called the constant of integration in your answer.  This is a letter, usually a ‘c’, that represents a number. 

Here are the basic rules for carrying out integration:

 

1.  If I integrate , I get

For example:

2.  Rule 1 holds for just about everything except when you have something to the power ‘–1’, i.e. ‘’, or ‘’ (these are the same thing).  In a special case like this, the integral of ‘’ is ‘’. ‘’ is the natural log.

3.  The integral of  is . 

4.  Integration can be done in bits.  Say I have  and I want to integrate it.  I can integrate each term separately, then add the results:

                                        First integrate  to get .    

                                         Then integrate  to get .

Note I have used a different letter to ‘c’ for the constant of integration.  Also note that I have used a different letter in each one – they do not necessarily have the same constant of integration value.

Add the results together:

                                                  

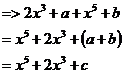
The ‘c’ in the final answer represents ‘a + b’.  Since ‘a’ is just a number, and ‘b’ is just another number, when they are added together they just represent yet another number.  To make it easier to read, we can just call this number ‘c’.

This method can also work when you have subtraction, or more than two terms.  However, you can only separate bits of a function that are separated by ‘+’s and ‘–’s – things which are terms.

Another way to approach this is to first go through the entire line and increase all the powers by 1:

                                                          

You then divide all the terms by their new powers:

                                                          

You then add the constant of integration:

                                                        

5.  The integral of  is .

6.  The integral of   is   (note the negative sign).

7.  If you have a linear function raised to a power, you can integrate it.  By linear function, I mean that there are not any squared terms or higher powers in it.

For instance:

                                                    Integrate

What you can do is represent the function in the brackets by a letter, say the letter ‘a’.  We can then rewrite what we have to integrate as. 

Integrate the letter normally – it becomes . ‘b’ is the constant of integration.  Then divide it by the derivative of the function a with respect to x. The derivative of function ‘a’ with respect to ‘x’ is calculated like this:

                                                        

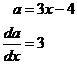
So if we divide our integral by ‘3’ we get:

                                                        

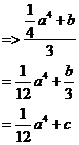
Since ‘b’ is just a number, we can rewrite ‘’ as ‘c’ to make the equation easier to read.

The last step is to substitute in what ‘a’ represents:

                                                     

And there is your answer.

There is a mathematical symbol that stands for the verb integrate.  Say I want to integrate ‘2x + 3’.  I can rewrite this without using words as:

                                                        

The integrate symbol is ‘’. I also need to say what variable I am integrating with respect to. This is what the ‘dx’ does – ‘dx’ means the change in ‘x’. It tells me that the variable I’m integrating is the one which is changing – ‘x’.

If I wanted to work out what it equals, I would just use the first integration rule and get the answer .