More simultaneous equations

Remember, equations may not always be given to you in the easiest form – they could look like:

To make these easier to solve, you could rearrange them into a more familiar form, like:

What if you have gaps in your simultaneous equations?  By gaps I mean you have a set of equations such as these:

There are no ‘a’s in the second equation, but this actually makes it easier to solve.  To write them in the standard form you could write them as follows:

Now they look like a standard set of simultaneous equations.  In this case, to solve them you could straightaway substitute b = 2 into the first equation:

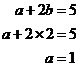
Solving three or more simultaneous equations

When you have more than 2 equations, the process is a bit more drawn out, but is still essentially the same.  We’ll use this set of simultaneous equations as an example:

                                         

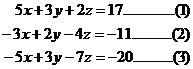
I am going to solve these using the substitution method. 

The first step is once again to get one of the equations in a form where there is just one letter on one side, let’s use equation 1.

                                          

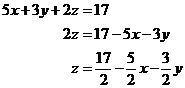
You then substitute this into one of the other two equations – let’s use equation 2:

                                     

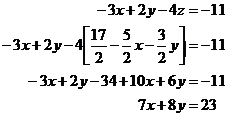
Now we have an equation with only two letters in it!  We want to eventually have an equation with only one letter in it.  We can do this by rearranging this two letter equation so there is only one letter on each side:

                                                      

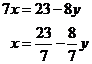
Through these two steps we have obtained two ‘new’ equations:

                                                   

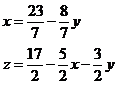
We can now substitute both of these equations into the equation 3:

                             

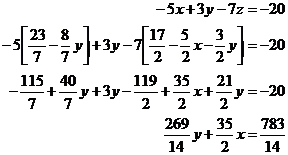
Note how we still have both ‘x’s and ‘y’s in this equation.  However, we can substitute

                                                       

into this equation again:

                                          

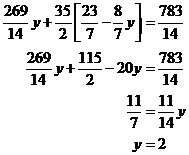
This example was deliberately chosen to show that even though there might be some horrible fractions involved in the calculations, the eventual answer can still be quite simple.  Now, to find out what ‘x’ and ‘z’ are we simply pick appropriate equations. 

An appropriate equation for finding ‘x’ is one which has ‘y’ in it, since we now know ‘y’, and just ‘x’ (no ‘z’s). 

                                                      

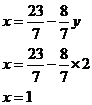
Now we can pick any equation that has ‘z’ in it, and substitute in the values for ‘x’ and ‘y’.  We can use the equation 1:

                                                 

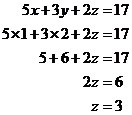
Notice how all the numbers came out ‘nice’ in the end – if you are getting horrible fractions in the calculations, you haven’t necessarily screwed up. 

If your calculator has the ability to do operations with fractions, learn how to use it well.  Try to keep your calculations in fractions rather then decimals, especially when you’re working with values like ‘one-third’ or ‘five-sevenths’, which can’t be represented exactly in decimal form.