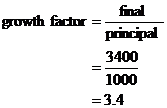Interest terms revision
First, a bit of revision:
Sponsored Links
Arithmetic progression
An arithmetic progression is any list of numbers that increase or decrease by a constant amount.
3, 6, 9, 12, 15, 18…
1, 0.5, 0, –0.5, –1…
Geometric progression
A geometric progression is any list of numbers that increase or decrease by a constant factor.
2, 4, 8, 16, 32…
10, 5, 2.5, 1.25…
Series
An arithmetic series is the sum of all the terms in an arithmetic progression. Similarly, a geometric series is the sum of all the terms in a geometric progression.
Some common terms and what they mean:
Principal: The initial amount of money invested, borrowed or lent.
Interest: In general, a charge on the money while it is being borrowed/lent.
Rests: The times when you stop to calculate interest.
Interest Rate: This is a measure of how much interest must be paid on the amount of money lent/borrowed. It is expressed in terms of a percentage of the principal that must be paid over a certain time length, usually one year.
Nominal Interest Rate: If the interest rate is given for a period which is not a year, the nominal interest rate is the rate which would equivalently apply over one year.
Final Amount/Amount: The final amount, or amount, is just the sum of the principal and the amount of interest built up over the time period.
Growth Factor: The growth factor is the ratio of the final amount to the principal.
Here’s an example:
|
John borrows $1000 from the bank, at a simple interest rate of 2% per month, for a period of 10 years. How much must he pay the bank in total to repay his loan? |
|
Solution |
|
The principal is $1000. The interest rate is 2% per month. The nominal interest rate is 24% per year. So every year, he owes the bank 24 % of the principal in interest. This is equal to 0.24 ´ $1000 = $240. This happens every year, so the total amount of interest he must pay back is 10 ´ $240 = $2400. The final amount he must pay back is the sum of the principal he borrowed at the start, plus all the interest he owes the bank. This is $1000 + $2400 = $3400. So he must pay $3400 in total back to the bank – this is the final amount. The growth factor is: |
Compound interest formula
If you want to know how much money you will end up after a certain amount of time using compound interest, you can use this handy formula:

So say I wanted to find out how much money I’d have after a year, on an initial investment of $1000, compounding monthly, at a yearly interest rate of 6%.
First thing, for this investment, interest is calculated every month, so I need to express the interest rate in terms of one month. I can do this by dividing the yearly interest rate by 12:
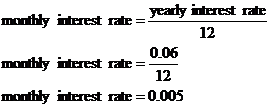
My principal is $1000, and I have 12 rest periods, so I can just plug numbers into my formula now:
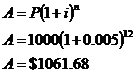
So after 12 months, I’ll have a total of $1061.68 – I will have earned $61.68 in compound interest.