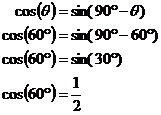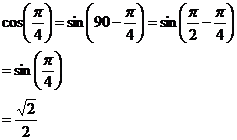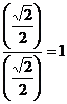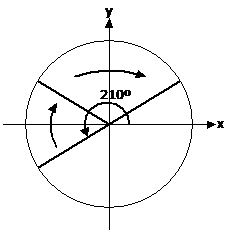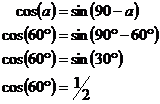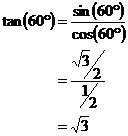Exact Trigonometric Ratios

When you take cos, sin or tan of some angles, you can express the answer as an exact number, rather than a decimal.  For instance,

                                                     

Sponsored Links

Try getting this answer using your calculator instead.  It will give you a decimal answer of around 0.86602540…  In many situations, the exact answer is better than the decimal answer.

Many angles have exact answers when you use sin, cos or tan on them.  These are summarised in the following table for cos and sin.  Remember that p radians is the same as 180°.

Angle in degrees

Angle in radians

sin(angle)

cos(angle)

0

0

0

1

30

p/6

45

p/4

60

p/3

90

p/2

1

0

The first thing to note is that there is a similarity between the cos values and the sin values.  The cos values are just the sin values, but in reverse!  So you don’t really have to remember the exact answers for cos, but just for sin.  You can get the exact answers for cos from this reverse trick.  The trick is easy to remember using  and

Exact trigonometric ratios question

Find .

Solution

I don’t know any exact answers for cos.  However, I have memorized the sin values, and I know that.  So I substitute the angle into this and get:

                                             

So this gives us answers for sin and cos.  What about for tan?

Well, tan is just as easy.  All you have to know is: .  You know all the sin answers off by heart.  From these you can get all the cos answers.  And if you know both of these, then you can get any of the tan exact answers.

 

Another exact trigonometric ratios question

Find .

Solution

We know straightaway that .  From this we can work out .

                                    

Tan is just sin divided by cos, which is just:

                                                         

This procedure may seem like it takes a while, but once you practise it a bit, you will get very fast at doing it.  It has the advantage that all you have to do is memorise 5 exact answers for sin, from which you can get everything else.

The table only had angles from 0° to 90°.  What about for angles from 90° to 360°?

These answers can be found using the unit circle discussed in the previous chapter.  It is all based around mirror reflections.  An example is the best way to demonstrate this.  Remember, all angles are measured from the positive x-axis, in an anti-clockwise direction.

Unit circle angle question

What is ?

Solution

First, draw this angle on a unit circle. Remember, all angles are measured from the positive x-axis, in an anti-clockwise direction.

Now we don’t know any exact answers for cos, sin or tan for angles larger than 210°.  However we can use ‘mirror reflection’ to get the answer.  First, ‘reflect’ the line over the x-axis.

Then, ‘reflect’ the line over the y-axis.

Now you have an angle in the 1st quadrant.  You should be able to work out the angle between the x-axis and the line is 30°.

Now all you do is work out . 

Only one more step before you have the answer – you must work out whether it is positive or negative. 

To do this, you work out whether sin is positive or negative in the two quadrants – the one 210° is actually in, and the one our final ‘reflected’ angle, 30° is in.  In this case they are the 3rd and 1st quadrants. 

Using the phrase “All Stations To Central”, we know that sin is negative in the 3rd quadrant, and positive in the 1st quadrant.  When the two quadrants have different signs, we change the sign of our answer – in this case from  to .  The answer is .

 

Another unit circle angle question

Calculate .

Solution

In this case, you only need one ‘reflection’ to get it into the 1st quadrant.  This reflection is across the x-axis.

The angle you get in the 1st quadrant is 60°.  What is tan 60°???

Well, we know that tan = sin/cos.  We know, because we have memorised it, that sin 60° is   We don’t know cos 60°, but we can get it:

                                             

This give us:

                                                 

Now all we have to do is work out the sign of the answer, positive or negative.  Tan in the 4th quadrant is negative, and in the 1st quadrant it is positive.  These are different, so we must change the sign.  The answer is therefore

                                                             

 

So to summarise, all you have to know is:

·         The value of sin for 0°, 30°, 45°, 60° and 90°

·         The fact that  and

·         The fact that

·         That you can ‘reflect’ angles not in the 1st quadrant until they are in the 1st quadrant, before you calculate sin, cos or tan of them.  The answer is obtained by comparing the signs of sin, cos or tan in the two quadrants – the quadrant the angle started in, and the 1st quadrant where it ends up after all the reflections. If they are the same, the answer is the same.  If they are different, the answer changes sign.