The unit circle

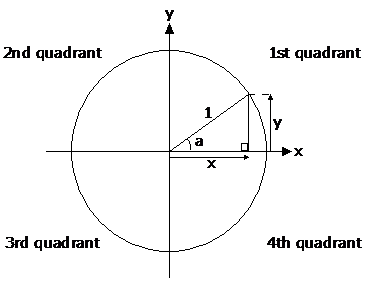
The unit circle is a circle with a radius of 1.  It is drawn on a set of axes so that its centre is at the (0, 0) point of the axes. One of the most important uses of the unit circle is in trigonometry.  You can see how by drawing a line from the centre of the circle to a point on the circumference like in the picture above.  Then draw a vertical line from that point on the circumference to the x-axis.  You have just drawn a triangle within the unit circle.  Now look at the angle marked ‘a’ above in the diagram.  What is sin a? 

Well, we know from SOH CAH TOA that sin is the opposite side divided by the hypotenuse.  The opposite side is of length ‘y’.  The hypotenuse is the radius of the circle, which means it is of length 1.  So sin a is ‘y/1’ which is just ‘y’! 

What about cos a?  Cos is the adjacent side divided by the hypotenuse.  The adjacent side is of length ‘x’.  The hypotenuse is of length 1 again.  So cos a is ‘x/1’ which is just ‘x’!

Finally, what about tan a?  Tan is the opposite side divided by the adjacent side.  The opposite side is of length ‘y’.  The adjacent side is of length ‘x’.  So tan a is ‘y/x’.

You can do this for all sorts of angles.  The above diagram is for an angle ‘b’ that is larger than 90 degrees.  Notice how the angle is always taken from the positive x-axis in an anti-clockwise direction.  Now say I want to find out what cos b is.

Cos is the adjacent side divided by the hypotenuse.  The adjacent side in this triangle is of length ‘x’.  The hypotenuse is the radius of the circle, and therefore is of length 1.  So cos b is x/1 which is just x!  Be careful! Since x is in the negative direction of the x-axis, cos b will be negative.

Let’s try tan b for this new triangle.  Tan is the opposite side divided by the adjacent side.  The opposite side is of length ‘y’.  The adjacent side is of length ‘x’.  So . Is tan b positive or negative?

Well, ‘y’ is in the positive direction of the y-axis.  However, ‘x’ is in the negative direction of the x-axis.

                               

So tan b will be a negative number.

A way to remember when cos, sin or tan is positive or negative is to remember the phrase ‘All Stations To Central’. In the first quadrant, All are positive.  In the second quadrant, only Sin is positive.  In the third quadrant, only Tan is positive.  And in the fourth quadrant, only Cos is positive.  You can of course make up your own rhyme!

There are also some important rules that are obtained from playing around with the unit circle.  They are:

                                               

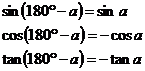
Radians

A ‘radian’ is another unit that you can use to measure angles. A radian is a lot larger than a degree – in fact there are about 57.3 degrees in a single radian. Radians are used because there are all sorts of neat things you can do with angles and trigonometry when you use them instead of degrees. The exact number of degrees in a radian is just: