There is one thing you should be careful of when you are using the sine rule to solve for angles in a triangle. Say we have the following triangle:

Sponsored Links
If you used the sine rule to solve for the unknown angle in this triangle, you’d get:
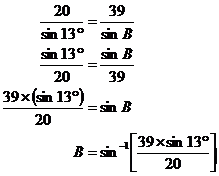
Note that sin-1 is another way of writing the inverse sine. If you plug this into our calculator and use its inverse sine function, you should get an answer like this:
B = 26 degrees
Now, looking at the original triangle, 26 degrees seems way too small an angle – and it is. There is a flaw in the sine rule based around the fact that:
![]()
Whenever you get an angle using the sine rule, you must check to see whether it makes physical sense – if it doesn’t then you must use the above rule to find the other possible answer:
![]()
An angle of 154 degrees is much more reasonable for angle B. It also means the sum of angles inside the triangle is 180°, so it looks like the correct answer.

