Inequations

From its name, you should be able to guess that inequations have something to do with equations. In fact, the name is exactly the same except for an ‘in’ at the front. Equations are where you have two expressions or sides, with an equals sign between them.  This means that the two sides are equal.  Well, the ‘in’ means ‘not’ in this case, so inequations have two sides or expressions that are not necessarily equal.

There are several types of new symbols that are used in inequations.  Here are some of them with an explanation of what they mean:

The larger than symbol: >

Example use:

                                                             

Whatever is on the left hand side of this symbol is larger than whatever’s on the right hand side.  For example, the first inequation is saying that “five is larger than three”.

The smaller than symbol: <

Example use:

                                                             

Whatever is on the left hand side of this symbol is smaller than whatever’s on the right hand side.  For example, the first inequation is saying that “three is smaller than five”.

The larger than or equals symbol: ≥

Example use:

                                                             

Whatever is on the left hand side of this symbol is larger than or equal to whatever’s on the right hand side.  For example, the first inequation is saying that “five is larger or equal to 3”.  Because it says “larger than OR equal” it means that the number on the right hand side can be either – it doesn’t have to be smaller, it can be the same value as the left hand side.  This means that there are two possible cases – one where the number is smaller, and one where the number is the same size.   is one case where the number is smaller.

The second inequation shows the other possible case where the numbers are the same size.  It says that “five is larger than or equal to five”.

The smaller than or equals symbol: ≤

Example use:

                                                             

Whatever is on the left hand side of this symbol is smaller than or equal to whatever’s on the right hand side.  Once again there are two possible cases.   is one case where the left hand side is smaller than the right hand side.   is the other case where the left hand side is equal to the right hand side.

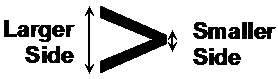
How to remember these symbols

If you look at these symbols you can think of one side being ‘big’ and one side being ‘small’.  The ‘size’ can be measured by the vertical size of the symbol at each side.  The ‘taller’ side is the bigger side, where the larger numbers are.

To remember the “…or equal to” symbols, you just have to look for the equals sign in the symbol.  Notice that it is always on the bottom part of the symbol, not the top part: