There are many situations where you have to find the solutions to an equation such as the following:
Sponsored Links
Now, if this had been a quadratic equation, you could simply plug numbers into the quadratic formula, and get a solution that way. But this equation’s first term is to the power 3, which means it is a cubed term, and quadratic equations can’t have any higher powers than a squared term.
This equation also can’t be simplified into a quadratic equation. In previous examples, sometimes the whole equation could be divided by ‘x’, to give a quadratic equation. In this case, if you divided through by ‘x’, then you would have ‘6/x’ as a term, and you would not have simplified it into a quadratic equation.
Divide through by x:
While it is almost a quadratic equation, the –6/x ruins any chances of it actually being one. So how do you go about solving such an equation? Remember by solving we mean finding the values of ‘x’ that make the equation true.
In cases like these, a combination of educated guesses and polynomial division must be used. Polynomial division is like normal long division, but instead of numbers, you use algebraic expressions.
First of all, we keep guessing values of ‘x’ which might make the equation true, and then try them out to see if they work.
Let’s try x = 0, and substitute into the left hand side
This does not equal the right hand side of the equation (0), so x = 0 is not a solution.
What about x = 1?
This does equal the right hand side of the equation, so x = 1 is one of the solutions to this equation. Now that we have one solution, we can carry out polynomial division to simplify the equation.
First we make a bracketed term, that will equal 0 when x = 1:
Now, we divide the original left hand side by this bracketed term, as follows:
To start off the division, think of something that you can multiply the bracketed term by to get an x3 term in the answer (in other words, to get the highest power term in the polynomial). What about x2:
This has an 
term.
So you multiply the bracket term by 
and write the result down
under your original polynomial. You then subtract the result from the original
polynomial, and get a new line, 
.
Now you perform the same process over again on the new line. Think of what you can multiply the bracketed term by to get a 5x2 term – what about 5x?
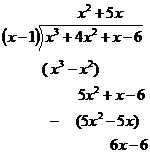
So you again multiply the bracketed term by the 5x, then subtract whatever that is from 5x2 + x – 6, and get 6x – 6. Then we again think of what we can multiply the bracketed term by to get a 6x term. What about 6?
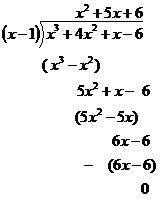
Now, for the last time, we multiply the bracketed term by the 6, and get 6x – 6. We then subtract this 6x – 6 from the 6x – 6 and get 0! When you end up with 0, the polynomial has divided perfectly. This is good! Now to explain what this all means.
The answer on top of the division sign, when multiplied by your bracketed term on the left of the division sign, gives the original polynomial we started with.
Now we’ve already guessed one solution, that is x = 1, because the left hand side bracket (x–1) = 0 when x = 1. And if that bracket equals 0, then 0 ´ (x2+5x+6) will equal 0, which satisfies our original equation. Now we have to work out the other solutions.
The other solutions will occur when the other bracket equals 0, so:
Now this should look familiar – it is just a simple quadratic equation – which we can solve very easily.
When it is solved, we find two more solutions, x = –2 and x = –3. So there are three solutions in total, x = 1, –2 and –3.
