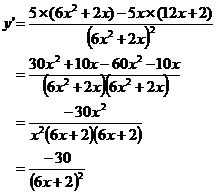This rule is for when you can split your function into one sub-function divided by another sub-function.  If the two sub- functions are u and v: 

                                                            

Then:

                                                       

Make sure you have v representing the sub-function on the bottom of the fraction, otherwise this rule won’t work. Here’s a sample question:

Quotient rule question

Find the derivative of

Solution

Firstly:                                                            Let u = 5x                                                       Let v = 6x2 + 2x. Which gives:                                                                                                                        Then:

When you get a derivative question, your first decision should be which rule to use.  You can then write your ‘u’s etc. out so they are easy to use:

Some students find it easier to just remember the product rule, and not worry about the quotient rule – any quotient rule problem can be turned into a product rule.  For instance, the last example could be converted into a product rule problem by changing the function to:

 is really . When we change it from dividing to multiplying, we change its power from 1 to –1.  In effect we are moving it from the denominator to the numerator – the sign of the power always changes when we do this.