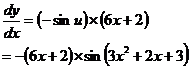The best way to demonstrate this is by example.
|
Sponsored Links |
|
Find the derivative of this function with respect to x: |
|
Solution |
|
Note that this function can be split into two functions: If we let that sub-function = u, or any letter we want, we can rewrite the function as: y = 4u5 where u = 3x + 4 All the chain rule says is that In words, this says the derivative of y with respect to x is equal to the derivative of y with respect to u times the derivative of u with respect to x. Note if you cancel out the ‘du’s on the right hand side, you are left with the left hand side. Now: And: So we can use our differentiation rules to calculate that We can then substitute in for what u is and give the answer as 60(3x + 4)4 |
Here’s another example question with trigonometric ratios.
|
Find the derivative of this function with respect to x: |
|
Solution |
|
Let u = 3x2 + 2x + 3. Then the function becomes y = cos u.
Let’s work out what each bit equals: And put it all together: |
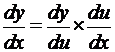 Now:
Now: