Rates of change

Rates of change are very important in mathematics.  Take for example the ‘speed’ of a car.  It is a measure of how far the car travels over a certain time, usually expressed in km/hr.  It literally means how many kilometres the car will travel per hour.  It could also be expressed in km/s or m/s or mm/day.  The important thing is that it is a measure of how much the distance changes for a certain change (increase) in time.

For instance, 100 km/hr says that for every change in time of one hour, the distance travelled changes by 100 km.

If you graph the distance travelled by a car on the y-axis, and the time taken on the x-axis, for some journey you might get a graph like this:

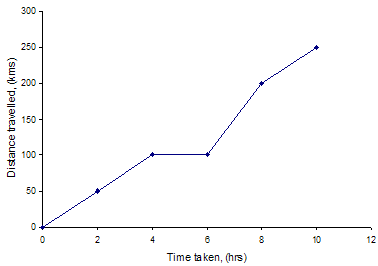
Now, for this graph (and any graph of distance vs. time), the gradient at any point represents the speed of the car at that time.  For instance, between hours 0 and 4, the car is travelling at 25 km/hr.  Between hours 4 and 6, the gradient is 0, telling us the car is not moving.  Then, between hours 6 and 8 the gradient is 50 km/hr.  Finally, between hours 8 and 10 the gradient is again 25 km/hr.  In general, the slope of a graph can tell us the rate of change of the y-axis variable, with respect to the x-axis variable.

What about for graphs with curves?

You can still find the rate of change the same way, but you have to draw a tangent to the point where you want to find the gradient, like follows:

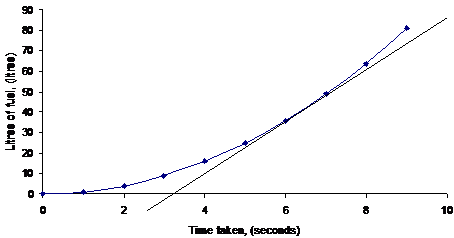
This graph shows a petrol tank being filled up at a gas station.  Now we know that the gradient represents the rate of change of the amount of fuel with respect to the change in time.  A steeper gradient means the change in fuel per second is greater.  Since the line gets steeper and steeper the tank is being filled at a higher and higher rate as time progresses.

Say we want to find the filling rate after 6 seconds.  We need the slope at that point.  We construct our own straight line parallel to the curved line at that point – called a tangent.  We then find the slope of our straight line and use that as our filling rate.  For this example, at time = 6 seconds, the filling rate is about 12 L/s.