There is one more method for solving a quadratic equation.  Say I have a quadratic function:

                                                   

You can use a process known as completing the square to solve it. First you divide the whole equation through by the coefficient of the  term (the coefficient is the number in front of the ):

                                                     

Then you move the constant (c) term over to the other side – the constant term is the one that doesn’t have any ‘x’s in it.  Remember the sign change!

                                                        

Then, whatever the number in front of the x term is (in this case 6), divide it by 2 (giving 3), then square it (giving 9).  Whatever the number is, you always divide it by 2 than square it.  Add this result to both sides of the equation:

                                                     

Now factorise the left hand side using the method discussed previously (forget about the 17, just concentrate on the left hand side of the equation.

                                                   

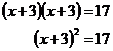
Take the square root of both sides, and remember to put a plus or minus sign next to the  to represent both possible solutions!

                                              

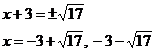
And there are your solutions for x which make the equation true.