This method can be used when you suspect that the solutions to the quadratic are ‘nice’ like in the last example.  It will not always find you a solution, but when it works it is quicker to use than the quadratic formula.  The best way to demonstrate is by example, let’s try a new quadratic equation:

                                                    

Now this is already in the general form, with a = 2, b = 6 and c = 4.  The first thing you do is think of ways to get , such as ‘2x’ times ‘x’.  You then write them down as follows:

                                                     (2x +  …) (x + …)

Now, to fill in the second part of each set of brackets, think of two numbers that multiply together to give c (which is 4).  Also, one of these numbers multiplied by 2x plus the other number multiplied by x must add to 6x.  This is more clearly demonstrated by example:

Possible pairs of numbers that multiply to give 4:

                                                             2 and 2

                                                           –2 and –2

                                                             1 and 4

                                                           –1 and –4

These all multiply to give 4.  Let’s try 2 and 2;

                                                      

To check whether you have a correct guess, multiply the brackets out:

                                                  

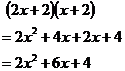
This gives  which is the correct quadratic equation.  If this was not the case we would have to go back and try different pairs of numbers.  If none of the pairs of numbers worked, we would have to go further back and find a different way to get , such as 4x multiplied by 0.5x, and then repeat the process. 

Now to find the solutions of what x must be, let the brackets = 0:

                                                   

All we have really done is rewrite the quadratic equation in a different form – it is still the same equation essentially.  Now we can easily solve it – for this new equation to be true, one of the bracket terms has to be 0:

Either (2x + 2) = 0 or (x + 2) = 0, because multiplying any number by 0 gives 0 – if one bracket is equal to 0, then it doesn’t matter what the other bracket is.

For 2x + 2 = 0, can rearrange:

                                                             2x = –2

                                                   x = –1 is one solution

For x + 2 = 0, can again rearrange:

                                                x = –2 is another solution

So the solution to this quadratic equation is x = –1, –2.  Note that these solutions are the same as for the first quadratic equation we saw.  Let’s compare them:

 

Equation 1

                                                     

Equation 2

                                                    

The second equation is just the first equation multiplied by 2!  

This is another good check to perform on a quadratic equation before you solve it – whether you can divide it by a number to make it simpler.  You solutions will still be correct as long as you divide everything through.  Be careful though – you want to still have all ‘nice’ numbers in your equation, you don’t want decimals or fractions left after you divide it.  And you can only do this when there is only one variable in the equation – don’t divide an equation like .

The quadratic equation also doesn’t have to be made up of ‘x’s – it can use ‘t’s, ‘q’s, or anything really.  But the process is still the same to solve them – don’t get put off by different algebraic letters.