This is what someone would call a typical quadratic equation.
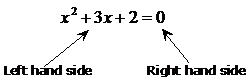
This equation simply says that “x squared plus three lots of x plus two must equal zero.” Now obviously, some values of x will make the equation true and some won’t. For instance, if we make x equal 2, then:
The equals sign with the line through it means “not equal to.”
When someone solves a quadratic equation, what they are doing is finding the values of x which make the quadratic (equation) true. True means the left hand side equals the right hand side. For the same equation, what about if x = –1? Then:
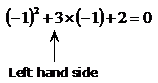
Remember that ‘–1’ squared is positive 1. This time the left hand side does equal 0 (the right hand side), so we have found a solution to this quadratic equation. The solution is
x = –1.
One of the important things to know about quadratic equations is that they often have two solutions. For the same equation what if x = –2? Then:
The left hand side is again equal to zero! So this quadratic equation has two solutions, x = –1 and x = –2. Don’t worry about how we got those solutions, we’ll get to that soon.
Now what happens if you get an equation like this:
This doesn’t look like a quadratic equation does it? But it is, if we rearrange it. The basic thing to keep in mind is that whatever you do to one side must be done to the other side as well. This is what we do for this equation:
Subtract 2 from both sides. That gives us:
Now add 3x to both sides:
This is now in the ‘normal’ quadratic equation form. Now it does look like the first equation, although with different numbers.
Anything that looks like this is likely to be a quadratic equation. The general form of a quadratic equation is:
The letters a, b, and c are just simply numbers. They can be fractions or decimals, negative or positive numbers. Any equation that fits this general form or can be rearranged to fit this general form is a quadratic equation. If a = 0 the equation changes from a quadratic equation into a linear equation – one that has no powers of squared or higher. However b and c can be zero. For instance, the following is a quadratic equation:
It doesn’t look the same simply because this equation has ‘b’ being 0. It is really:
These types of quadratics are the easiest to solve – the answer in this case is just ±2. Remember the plus or minus – the answer is both 2 and –2. Don’t confuse this with:
The square root of 4 is just 2, not –2.
You only get plus or minus answers when you have the
following situation: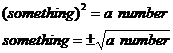 
If only c = 0, then you can get an equation like:
This case has an obvious solution – x = 0 makes it true. To find the other solution, divide both sides by x (remember 0 divided by anything apart from 0 is just 0):
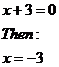
So this gives us the two solutions x = –3, 0.
Another situation in which a quadratic equation occurs is
the following: . 
Now a quadratic equation must have no higher powers
than a squared term. This one has a term to the fourth power. But what if we
make up a letter 
? Then we can rewrite this equation
as
Now this is in the standard quadratic equation form.
In general, it is good to have an equation in this form because they can almost
always be solved quickly. So you would solve this equation for X, then solve
for x in 
.
We’ll deal next with ways to solve quadratic equations.