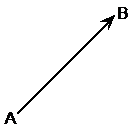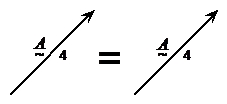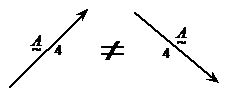Vectors

Scalars are things which just have a value – for instance ‘5’ is a scalar quantity – all it has is a value of ‘5’, it doesn’t have any other characteristics or properties.

Vectors have both a magnitude value and a direction – so they’re made up of two things.  An everyday example of a vector quantity is if you are describing the movement of a ship or plane.  You might say something like, “the plane travelled 2000 km north.” You could represent this movement on a diagram by an arrow, like this:

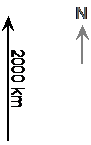
This is a vector quantity because it has a magnitude (2000 km) as well as a direction (north).

There are two main ways to talk about a vector – you can either describe the two points the vector points between, or just name the whole vector one thing:

In this case, we can describe this vector as  or . The arrow above the AB or the tilde sign below the AB tells us that it’s a vector.	If we just name the whole vector using one letter, then we can describe it using the letter with a tilde sign underneath it to tell us it’s a vector, like this:.

Vector magnitudes

Sometimes we want to talk about only one of the two parts a vector is made up of, so only one out of the magnitude or the direction.  A common example of this is when we’re talking about how far someone might have walked – we don’t necessarily care which direction they walked, but just how far it was.  Say we had a person who walked 15 km in the direction west.  The vector showing their walk would be:

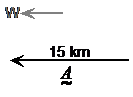
To talk just about the magnitude of this vector, but not the direction, what you can do is write the vector letter down and put a pair of vertical lines around it:

                                                        

When we talk about the entire vector, then it would look something like this:

                                                     

Notice how now we’ve described not only the distance but the direction of travel as well.

Equal vectors

For normal numbers to be equal, they have to have the same value.  For instance, .  For vectors to be equal, they have to have the same magnitude and the same direction:

Taking the negative of a vector

If you put a negative sign in front of a vector, you reverse its direction.  It keeps the same magnitude however.  So if I have:

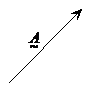
Putting a negative sign in front of my vector makes it reverse direction.  So if I wanted to draw , I’d get:

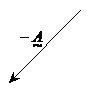
Multiplying a vector by a scalar

If you want to change the magnitude but not the direction of a vector, you can multiply it by a scalar.  Any scalar larger than 1 will make the vector longer, any scalar smaller than 1 will make it shorter.  For instance:

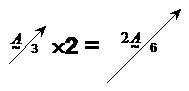
The  vector has a magnitude of 3.  When we multiply it by a scalar value of 2, the magnitude doubles in size, but the direction remains the same.  So we get a new vector, , with a magnitude of 6, but with the same direction as the original vector.