So far we’ve covered adding, subtracting and multiplying matrices. We’ve also gone over how you can multiply or divide any matrix by a scalar value (single value). Dividing matrices by other matrices is a different sort of thing however. You don’t just go and divide one matrix by another. One thing you can do however is find the inverse of a matrix.
Say I start with a 2 by 2 matrix, matrix A:
The inverse of this matrix is the matrix you need to multiply it by to get the identity matrix. It’s just like for actual numbers, for instance, say we want to find the number that we multiply 6 by to get 1:
We know that the fraction ‘one sixth’ goes where the question mark is:
is known as the inverse of 6 – it’s
the number you multiply 6 by to get 1. Well, with matrices, the only
difference is that instead of ‘1’ we have the identity matrix, which is the matrix
equivalent of 1. So we can write the inverse equation for our matrix A
like this:
Since our first matrix is 2 by 2, and our answer is 2 by 2, the matrix which is going to go where the question mark is will be 2 by 2 as well:
How do we find our inverse matrix?
Finding the matrix inverse
For a two by two matrix, it’s fairly easy to find its inverse matrix. If we have a matrix called A:
We can find the inverse like this:
The inverse of matrix A is written with a power of –1; 
. Notice how the
‘a’ and the ‘d’ have swapped places, and also how the sign of ‘b’ and ‘c’ has
changed. The ‘ad – bc’ part in the denominator of the fraction is called the determinant
of the matrix A, and is often written as 
or 
:
So if we go back to our original A matrix, we can find its inverse using this information. First of all, let’s work out the determinant of this matrix:
Next, we need to swap around and change signs of the elements in matrix A:
So our inverse of A is:
Now that we’ve found our inverse, we can check whether when we multiply A by it we really do get the identity matrix:
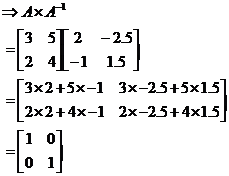
It works – 
really does give the identity
matrix. So how is this useful? Well, one of the most common uses of matrices
is to solve simultaneous equations. Say we had these two equations and we
wanted to solve for the values of x and y:
We can convert these equations into matrix form like this:
When these matrices are multiplied out, you end up with the equations we started with. Now, with any equation, you can do whatever you want to one side of the equation, as long as you do it to the other side. In this case, multiplying both sides by the inverse of the first matrix gives you a very useful result. We’ve already worked out the inverse of this matrix, so let’s go ahead and just do the calculation:
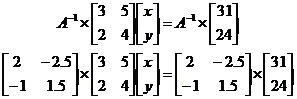
Then actually do each of the individual calculations:
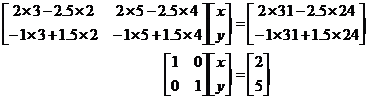
We could have skipped a lot of these steps because we already knew that when we multiplied the inverse matrix by the original matrix we’d just get an identity matrix, like we now have in front of the ‘x and y’ matrix.
By doing the same thing to both sides of the equation, we’ve made it a lot simpler. If we multiply out the matrices now, we get this:
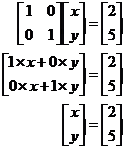
By multiplying out the matrices we get a very simple answer for the two variable values:
