The term ‘identity matrix’ is used to describe any square matrix (same number of rows as columns) which has ones down its primary diagonal, and zeros everywhere else. The primary diagonal starts at the top left corner of the matrix and continues down to the bottom right corner. For instance, these are both identity matrices:
![]() ,
, 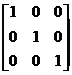
Sponsored Links
The identity matrix is usually named ‘I’. Also, the subscript of I (a little number to the right and below the ‘I’) is used to describe how large the identity matrix is:
![]() ,
, 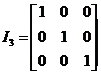
Now what does the identity matrix do? Well, it’s just like the number ‘1’, but for matrices. Now, we know that any number we multiply by ‘1’, we just get the same number again, for instance:
![]()
Well, any matrix you multiply by an identity matrix, you just get the original matrix again as your answer. Of course you have to pick the correctly sized identity matrix so you can actually do the multiplication. Here’s an example:
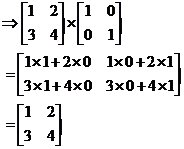
Notice how we just get what we started with.

