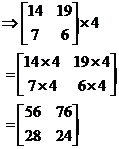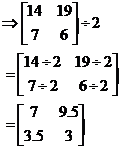Adding and subtracting matrices
You can only add or subtract one matrix with/from another if they have the same order – the same number of rows and the same number of columns. To actually do the calculation, all you do is perform the addition or subtraction on each pair of corresponding elements (the elements in the same position as each other):
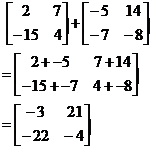
Sponsored Links
It pays to be careful when you’re doing matrix calculations, because it’s very easy to lose track of which element matches up with which, especially when the matrices get larger and your eyes get tired.
Multiplying matrices
Multiplying matrices is quite a bit more complicated than adding or subtracting. First of all, the matrices don’t necessarily have to have the same order. What does have to happen is that the number of columns in the first matrix has to equal the number of rows in the second matrix. Why? Well, let’s show you how multiplication happens and then it will all become clear. Let’s do this calculation:
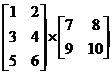
To do multiplication, you start at the top row of the first matrix, and multiply each of these elements by the ones down the first column of the second matrix. So the ‘1’ multiplies the ‘7’, and the ‘2’ multiplies the ‘9’. These two answers are added together to give you the value in the top left of your new matrix.
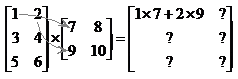
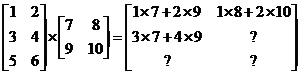
It helps to work out what the order of your answer
matrix is going to be. The number of rows in your new matrix will be
equal to the number of rows in your first matrix. The number of columns
in your new matrix will be equal to the number of columns in your second
matrix. So in this case, our first matrix has 3 rows, so our answer will have
3 rows. Our second matrix has 2 columns, so our new matrix will have 2
columns. So its order will be ![]() .
.
The next step in the calculation is to stick with the same row in the first matrix, but multiply it by the elements in the second column of the second matrix, like this:
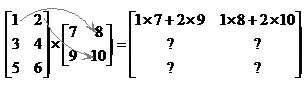
Now we’ve finished with the first row in both our first matrix and our answer matrix. We move on to the second row of our first matrix. The first step is to multiply it by the first column of the second matrix:
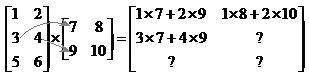
Then we multiply the same row by the second column in the second matrix. That finishes us with the second row in both the first matrix and the answer matrix. Then we move on to the last row in our first matrix and finish off the calculation. The matrix you should end up with is:
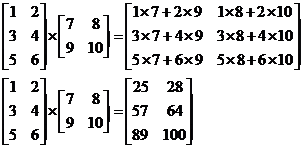
Multiplying and dividing by a scalar
An easier multiplication or division operation to perform is multiplying a matrix by a scalar. A scalar is a single number, rather than a group of numbers like in a matrix. All you do is perform the multiplication / division individually on each element in the matrix. For instance, take these two operations:
|
|
|