Matrices

A lot of people don’t ever cover matrices during their schooling, but it’s worth at least knowing some of the very simple stuff about them.  Just so you know that there’s more to matrices then the movie “The Matrix”!

A simple matrix is a two-dimensional clump of numbers.  It has a length and a height.  For instance, this is a two by three matrix:

                                                    

The first dimension mentioned is the number of rows – two. The second dimension mentioned is the number of columns – three.

The order of a matrix

When you describe the size of a matrix, you always describe the number of rows first, then the number of columns.  This matrix has two rows and three columns, which is why it’s described as a two by three matrix.  This is often called the order of the matrix – the number of rows by the number of columns.

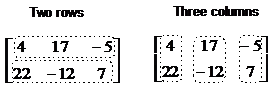
In a two by three matrix, there are six elements – cells or places where a value is.  The elements in this matrix are 4, 17, –­5, 22, ­–12 and 7.

Describing an element

Sometimes you want to point out a certain element to discuss.  For instance, if I wanted to point out the ‘22’, I could say something like the number in the 2^nd row, in the 1^st column.  A more formal mathematical way is to give the matrix a name, such as ‘A’, and then specify elements in the matrix by using two subscript numbers. Subscript numbers are tiny numbers written to the right and below of normal size numbers. First let’s give our matrix a name:

                                                

The order of the subscripts we use is important – we specify the row number is written first followed by the column number.  And we always count from left to right and from top to bottom.  So the 22 could be described in this way:

                                                          

This says that the value in row 2, column 1 of matrix A is equal to 22.  To talk about the ‘–5’ element we’d say: