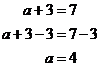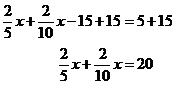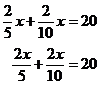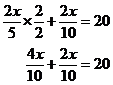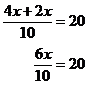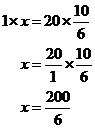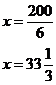Equations

You probably heard about equations a long time before you actually had to do anything with them.  So what is an equation?  Well, we can look at the word equation to work this out. Equation is similar to the word “equals”.  Equations are mathematical expressions that show one thing is equal to another.  For instance, the following is a very, very simple form of equation:

                                                          

Everyone knows that “two times five equals ten”.  But when you write it down, with an equals sign there, what you have done is write an equation.  More often, equations will look something like this:

                                                          

Most equations have at least one algebraic variable in them.  Usually in questions you have to solve for the value of the algebraic variable, or in other words, work out what its value is.  To do this you need to try and get the algebraic variable by itself in the equation.

Equations have the following sort of general layout:

                                         Left Hand Side = Right Hand Side

Or

                                                      L.H.S. = R.H.S.

Now the most important thing to remember when you’re working with equations is:

You can do anything to one side of an equation, as long as you do it to the other side as well.

 

So let’s go back to our simple example:

Simple equation question

Solve

Solution

I want to get the ‘a’ all by itself.  At the moment there is a ‘3’ on the same side as the a.  To get rid of the 3, I could subtract 3, remembering that whatever I do to one side I have to do to the other side as well:                                                       So in this calculation I have subtracted 3 from both sides of the equation, and then done some simple subtraction.  And there’s my answer – ‘a’ is 4.  Although this was a very simple example, the basic principle applies for very complicated equations as well.  You’ve just to remember to do the same thing to both sides of the equation.

So let’s jump straight in and solve a complicated equation.  For the following equation, we’ll try and work out the value of x:

More complex equation question

Solve

Solution

Now remember that we’re trying to get the algebraic variable all by itself on one side of the equation.  At the moment we have terms with ‘x’ in them on both sides of the equation.  It would be good to get rid of one of these terms.  Let’s try and get rid of the  term.  To do this, all we need to do is add  to both sides of the equation like this:                                                     Add  to both sides:                                          On the right hand side of the equation, the two ‘x’ terms cancel out, so we’re left with:                                                     I’ve also ­rearranged the order of the terms on the left hand side so that the ‘x’ terms are next to each other.  So now we’ve at least got all the x terms on the same side of the equation.  Unfortunately, there’s an annoying ‘-15’ hanging around on their side too.  We can get rid of this ‘–15’ by adding 15 to both sides of the equation:                                              Now we’ve got only ‘x’s on one side, and only numbers on the other.  It would be good if we could combine the two ‘x’ fractions into one single fraction.  To do this we need to put each fraction over the same bottom (denominator) number.  To make it a little bit clearer first, we can write the ‘x’ on the top of the fraction, which means exactly the same thing as writing it to the side of the fraction:                                                       Now, to get the same denominator for both fractions, let’s change the  fraction so it has a denominator of 10.  We can do this by multiplying its top and bottom by 2:                                                     Now that we’ve got both fractions with the same denominator, we can add them together:                                                         This leaves us with ‘x’ being multiplied by a fraction.  The fraction  is often called the “coefficient of x”.  We want ‘x’ all by itself, so we want to get rid of that fraction in front of it. To get rid of something that is multiplying the algebraic variable, divide both sides by it.  So in this case, we can divide both sides by :                                                    The left hand side of this equation is easy to work out – if you divide something by itself, you are left with 1.  So the left hand side becomes “1 times x”:                                                        The right hand side we can turn into a multiplication, by swapping the numerator and denominator of the equation:                                                        After a bit of multiplication, we are left with an improper fraction.  Usually, it is best to give answers as mixed numbers, so let’s turn this into a mixed number.  We can either do this using the calculator, which was explained in the fractions section, or by hand.  Since we’re mainly focussing on equations and not fractions in this section, I’ll ‘cheat’ and use my calculator:

Checking equation solutions

Now the best way to check an equation is to take the value you work out, and substitute it back into the equation to see if it still makes sense.  So, using the previous example, I’d take  and substitute it back into the equation where the ‘x’s were:

                                          

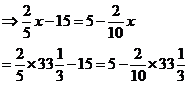
Best to pull out the calculator to solve this one:

                                         

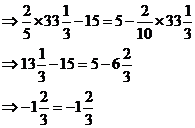
If we work through and simplify each side of the equation to just a single number, we get that the left hand side is equal to the right hand side.  This means the equation is true when , so we have found the right answer.

Equations with brackets

Sometimes equations have brackets in them.  Usually it’s best to multiply out or expand the brackets and then solve the equation as you normally do.  For instance, if I had the following equation to solve:

                                                     

Then I’d be best off expanding the brackets first, and then solving the equation:

                                                     

Now I can solve the equation as normal.  I want to get all the ‘x’s by themselves on one side.  At the moment they’re on both sides of the equation, so I’m gonna get rid of the ‘x’ on the left hand side by subtracting ‘x’ from both sides:

                                                 

Now I just have to get rid of the 6 which is on the same side as the ‘x’.  I can do this by subtracting 6 from both sides of the equation:

                                                     

And there’s my answer – x is equal to negative one.  It doesn’t matter which side your algebraic variable ends up on, as long as it’s all by itself.

                           “” means exactly the same thing as “”

In some special cases, it’s better not to multiply out the brackets.  For instance, say I had the following equation to solve:

                                                      

Now, you only need brackets when there’s something multiplying everything inside them.  In this case that something is the number ‘5’.  If I could somehow change that ‘5’ into a ‘1’, then I wouldn’t need the brackets anymore.  This is because nothing changes if you multiply something by 1. 

                     is the same as  which is the same as

So how can I change this ‘5’ into a ‘1’?  One way to do this is to divide it by 5, because 5 divided by 5 gives you 1.  But remember, what you do to one side of the equation you have to do to the other as well.  But can I divide the other side of the equation by 5 easily?  In this case, I can – 35 divided by 5 gives you 7.  So let’s do it:

                                                    

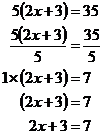
Now I’m left with a very simple equation to solve.  I just need to get rid of the 3, and then the 2 in front of the x:

                                                    

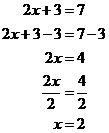
And there’s the answer.  So sometimes you can solve the equation without having to multiply out the brackets.  You need to keep an eye out for equations which can be solved without expanding out the brackets.