One very common exponential relationship is the base 10 one:

                                                           

The graph of this function is:

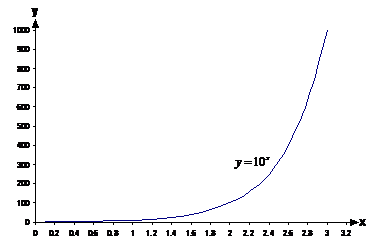
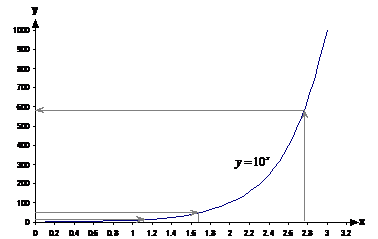
This graph can be used to write numbers as a power of 10.  For instance, the number 500 – we know it’s somewhere in between  and .  By tracing a horizontal line across from 500 on the y-axis until it intersects the line, then tracing a vertical line downwards to the x-axis, we can find the approximate power that will give us 500:

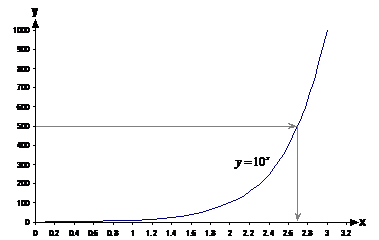
Seems to line up with about x = 2.7 on the x-axis.  You can check this using your calculator:

                                                       

Not bad hey!  You won’t always get answers quite this accurate, but they should be pretty close.

Multiplying using an exponential graph

Multiplying two numbers like 47 and 13 isn’t an easy task for some people.  What you can do is use an exponential graph to get the answer.  The graph makes it easier by turning it into a multiplication problem with two powers.  For instance, we find doing something like this very easy, because all we do is add the powers:

                                                        

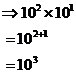
So if we can find what powers we’d need to create the numbers 47 and 13, we could add them together and then look up our answer on the graph.  So let’s start by finding the powers that we raise 10 by to get 47 and 13:

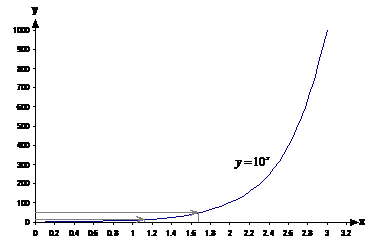
Because of the scale on the y-axis, it’s hard to get the exact position of 13 and 47, but do your best.  In this case, I’ve got about 1.11 for 13, and about 1.66 for 47:

                                                     

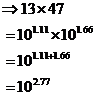
Once we’ve got our answer in ‘power of 10’ form, we can look it up on the graph to get our actual number answer.  This time we start at the x-axis at x = 2.77, and trace vertically upwards till we hit the line.  Then we trace horizontally across to the left until we hit the y-axis:

The line ends up hitting the y-axis around 585, which is our answer for what 47 multiplied by 13 is.  If we use our calculator to get the actual answer, we find that it is 611, that’s about a 4% error, which is pretty good considering all the inaccuracies there are trying to read values off the graph and draw straight lines between points.

Dividing using an exponential graph

To do division it’s the same process basically, except that you subtract the powers instead of adding them.  For instance, if I was doing:

                                                          

After doing the graph stuff, I might convert this statement into something like this:

                                                       

This time because it’s division, we subtract the second power (the power of the number doing the dividing) from the first power (which is the power of the number being divided):

                                                     

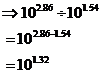
Then you’d look that up on the graph to get the exact number value. Using the graph I get an answer of about 20, which is fairly close to the correct answer of 23.3 (I haven’t actually drawn this one in on the graph).