Say you’re given something like this:
Because we know that 8 is a power of 2, we can work out
that 
.
Because there’s only one unknown variable (‘a’), then we only need one
piece of information to work it out. Sometimes however we might be given
something like this:
|
x |
10 |
15 |
20 |
|
y |
124.4 |
668.9 |
3598 |
A question might ask you to find ‘a’ and ‘b’. The trick in a situation like this is to look at the factor between two y values. We can compare the values of y for x = 10 and x = 15 for instance:
Notice how the ‘a’ doesn’t change between the lines. The only thing that changes is the value on the left hand side of the equation, and the power that ‘b’ is raised to. What we can do is divide the second equation by the first equation:
It’s very neat – we get a new number on the left side of the equation. On the right side, the ‘a’s cancel out, and so do a lot of the ‘b’s.
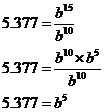
To work out what ‘b’ is, we can raise both sides of the equation to the power 0.2:
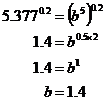
Now to work out ‘a’, we can take any of our data pairs. Let’s use the first pair of data values – x = 10 and y = 124.4:
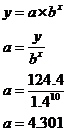
So our overall equation that describes the table data is:
We should check that the equation we got using the information from the first two pairs of data fits the other data in the table – in this case the last pair of data when x = 20:
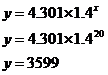
This is close enough to the value of 3598 in the table, the difference is due to rounding errors.