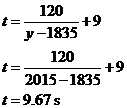When you plot a normal inverse relationship like ![]() , you get a curve
like this:
, you get a curve
like this:

Sponsored Links
This graph has two asymptotes - the straight
vertical and horizontal lines the plotted line never gets to touch. The vertical
asymptote is the vertical line along the y-axis. The horizontal
asymptote is the horizontal line along the x-axis. Now, by modifying the ![]() equation you can
shift this graph up or down and left or right. The general modified form of
the equation is:
equation you can
shift this graph up or down and left or right. The general modified form of
the equation is:
![]()
‘a’ is how many units the graph has been shifted to the right, and ‘b’ is how many units the graph has been shifted upwards. If you set ‘a’ and ‘b’ to equal ‘0’, then you just get the original equation and graph shown above. But say we set ‘a’ to ‘5’ and ‘b’ to 1, then we get this graph:
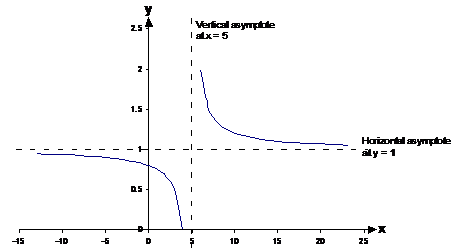
See how the graph has shifted 5 units to the right and 1 unit upwards. The asymptotes too have moved – the vertical asymptote has moved 5 units to the right, and the horizontal asymptote has moved up 1 unit.
Men’s running speed in the 100 metre sprint
Generally speaking people are much better at sport than they were 50 years ago. Training has improved, nutrition is better and nowadays doing sport is a job for many people rather than a spare time thing. The times in the 100 metre sprint for men have gradually dropped over time.
|
Year, (y) |
Time, (s) |
Year, (y) |
Time, (s) |
|
1912 |
10.6 |
1988 |
9.92 |
|
1921 |
10.4 |
1991 |
9.9 |
|
1930 |
10.3 |
1991 |
9.86 |
|
1936 |
10.2 |
1994 |
9.85 |
|
1956 |
10.1 |
1996 |
9.84 |
|
1960 |
10 |
1999 |
9.79 |
|
1968 |
9.95 |
2002 |
9.78 |
|
1983 |
9.93 |
|
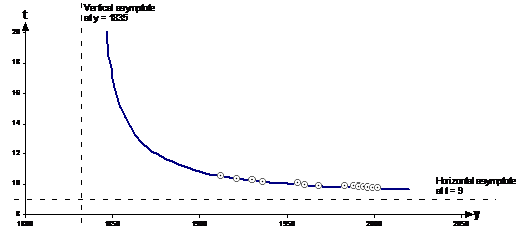
Fit a curve to the data and predict what the fastest possible time men will ever run for this event. Calculate the predicted time for 2015. To help you plot the curve, use this for the equation: ‘a’ and ‘b’ you’ll have to work out for yourself. |
|
Solution |
|
First we need to plot the data on a graph, like this:
We can draw in how we think a curve would best fit this data, and extend the curve to find the two asymptotes.
Drawing a curve that fits the data involves a bit of practice and experience with what ‘looks right’, and it’s never going to be perfect. Same with guessing where the two asymptotes are – just try to get something that looks reasonable. In this case, the asymptotes are at y = 1835 and t = 9.0. We can use this asymptote information to create our relationship equation between ‘t’ and ‘y’. The relationship given to us in the question was: Don’t be confused by our ‘y’ variable being on the x-axis (horizontal axis), when it’s normally on the vertical axis. The ‘y’ variable in our question is the year, and has nothing to do with the ‘y’ in normal x-y relationships. ‘a’ corresponds to the vertical asymptote – at y = 1835. ‘b’ corresponds to the horizontal asymptote – at t = 9.0. So: The answer to the first part of the question can be found by looking at the meaning of the asymptotes. The vertical asymptote at y = 1835 doesn’t really have any meaning, although it implies that if the races had been run back that far in time, the time taken to complete 100 metres would have become very, very long (which isn’t realistic, but that’s OK, since predicting times that far back in time is rather severe extrapolation and is outside the bounds of our model). The horizontal asymptote has plenty of meaning however – t = 9.0 seconds. The graph never actually gets to touch the horizontal asymptote – which means that in the future times will get closer and closer to 9.0 seconds but never get there. So that’s the answer to the first part of the question – according to our model the fastest time that will ever be run will be just above 9.0 seconds. The second part of the question just means using the equation we’ve found directly: So according to our hyperbolic model, in 2015 the world record for the men’s 100 metre sprint will be around 9.67 seconds. One thing to note for this question – because the process of drawing the curve to fit the data is so approximate, the answers you get are not going to be very accurate. If you did the question again, you might draw quite a different curve, with different asymptotes, and as a result get significantly different answers. |