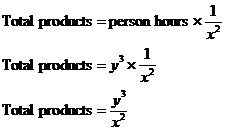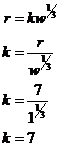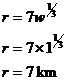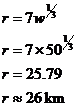First of all, you’re looking for a relationship between two different variables, for instance ‘x’ and ‘y’. There can be other ‘letters’ or ‘symbols’ in the equation, but only if it is said somewhere that they are constant values (they do not change, unlike the values of variables).
You’re also looking for something which only has two terms – one on each side of an equation. Sometimes you might have to do some rearranging before you can get an equation into this form. For instance, say we were given:
Sponsored Links
We could rearrange this by multiplying both sides by y2:
In this form we can clearly see that it is a direct square relationship, since it’s in the form:
However, if we were given this equation:
There are three terms in this equation. However, we can simplify it by moving the 3 over to the other side, and then multiplying both sides by y2:
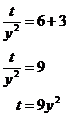
And once again we’ve got a direct square relationship. There can be direct relationships which aren’t nice squares or cubes too:
If we square root both sides, this is like multiplying each power by 0.5, so we get:
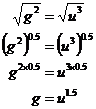
This is still a direct relationship, but is halfway in
between a direct linear relationship (which would be 
) and a direct square
relationship (which would be 
).
Something like 
doesn’t work out to be a direct
relationship however. If you get the ‘x’s all on one side and the ‘y’s on
another, you get this:
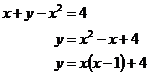
To be a direct relationship, we need to be able to
write the equation in a form like 
or 
, or 
or even perhaps 
. No matter how much you
rearrange this equation, you’re not going to be able to get it into one of
these general forms. What’s stopping you is both the ‘–x’ and the ‘4’ in the
second last line. If you got rid of those, then you’d just have:
and your ‘k’ constant would be ‘1’. But because of the ‘–x’ and ‘4’, it’s not a direct relationship.
The ‘x’ people make ‘x’ products problem
This is a classic problem, which always bamboozles people the first time they get asked it. Here it is:
|
If x people in a factory make x products working x hours a day for x days a week, how many products do y people make working y hours a day for y days a week? |
||||||||||||||||||||||||||||||||
|
Solution |
||||||||||||||||||||||||||||||||
|
“That’s easy!” most people say. They’ll just make ‘y’ products. WRONG! This is a deceptive question. Think about it this way. Say ‘y’ was a number half as large as ‘x’. Then they’d be half as many people working – that would halve the number of products. But they’d only be working half as many hours a day – that would halve the number of products again. And they’re only working half as many days a week – that would halve the number of products yet again. So saying that they’d produce ‘y’ products is wrong – they’d be producing a lot less than half as many products as the ‘x’ group of people. A more mathematical way of approaching this problem is to work out how many products one person working one hour a day, for one day a week produces. Then you just scale it up for y people working y hours a day for y days a week. So let’s start:
Let’s reduce the number of people to ‘1’. This is a reduction from ‘x’ people to ‘1’ person. This means the number of products will reduce by a factor of ‘x’ as well:
Now let’s reduce the number of hours/day to just 1. This will again reduce the number of products produced by a factor of ‘x’:
Last thing to do is reduce the number of days/week to just 1. Once again the number of products produced will reduce by another factor of ‘x’:
So one person, working for one hour a day for one day
a week will produce We want to know how many products ‘y’ people working
‘y’ hours a day for ‘y’ days a week will produce. If we can work out how
many person hours this is, we can just multiply that by In this case it’s pretty easy to work out the number of person hours – it’s just the number of people times the number of hours a day times the number of days a week: So they work This question is a good example of how, “if it looks too good to be true, it probably is.” The answer that springs to mind straight away is not necessarily correct. It’s always worth thinking about a question for a bit before answering. |
products. One hour a day for one
day a week is just one hour total per week. We can call this ‘1 man hour’ or
‘1 person hour’. This is a commonly used term in the workplace – the amount
of work that 1 person does working for one hour. We know that 1 person hour
will produce 
hours a week in total. So the
total number of products they produce is:
Nuclear weapons effects
A nuclear weapon is a very powerful weapon, which can destroy whole cities. The strength of a nuclear weapon is usually measured in kilotonnes (thousands of tonnes) or megatonnes (millions of tonnes) of TNT that would be required to produce an equivalent explosion. A typical modern nuclear weapon might be around 1 megatonne, although ones as large as 60 megatonnes have been produced.
One of the things most people don’t realise about nuclear weapons, is that in practical terms a 10 megatonne weapon is not ten times as powerful as a 1 megatonne weapon. For instance, a 1 megatonne weapon will severely damage or destroy houses out to a radius of about 7 km from the centre of the explosion. For a 10 megatonne weapon this radius does not increase by a factor of 10 to 70 km, but a factor of about 2 – to about 15 km.
|
Here is some approximate data for the radius within which severe damage is done to brick houses for various size weapons. Work out what type of relationship there is between weapon size and damage radius, and work out the exact relationship. Comment on why countries haven’t bothered building larger individual weapons since about the 1960’s.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Solution |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Obviously, as the size (measured in equivalent tonnes
of TNT) increases, the damage radius goes up. It’s also definitely not a
linear relationship – when the size of the weapon goes up by 10 times, the
damage radius only seems to double. We can call the equivalent tonnage of
the weapon ‘w’, and the damage radius ‘r’. We can check what type of
relationship exists by trying various ratios like
Hmmm…seems like as the powers of ‘w’ on the denominator get higher, we’re getting further away from having the same values all down the column. What about if we go in the opposite direction and try fractional powers:
After messing around trying some of the simpler
fractional powers, it appears that the ratio To work out the exact equation that describes the data in the table, we need to find the ‘k’ value in this equation: We can do this by picking one of the data pairs in the table, I’m going to pick the 1 MT, 7 km data: So the approximate formula for the severe damage radius of a nuke is: where w is the equivalent TNT tonnage of the weapon in millions of tonnes, and r is the radius in kilometres. The comment part of the question shouldn’t take too much thinking about. Say we tried to build a 50 MT bomb. Let’s compare it with a 1 MT bomb. The damage radius for a 1 MT bomb and a 50 MT bomb can be calculated this way (or taken from the table):
So for a bomb with fifty times the equivalent tonnage of TNT, you only get about 4 times as large a damage radius. Now, bear in mind that these military types are really concerned with the area of damage – so for a radius four times as large the damage area is sixteen times as large (remember the area of a circle is dependent on the square of the radius, so a doubling in radius results in a quadrupling in area). But it’s still not fifty times larger. What the generals are better off doing is building fifty 1 MT bombs. That way you do get fifty times the damage area of one single 1 MT bomb, but with only a total equivalent TNT tonnage of 50 MT. This is part of the reason the superpowers stopped trying to make larger and larger individual nukes – the small increases in the damage capability of the weapons wasn’t worth the huge amounts of money and resources required. |
or 
. To make everything
consistent, let’s express all the tonnages in megatonnes, and all the
radii in kilometres:
