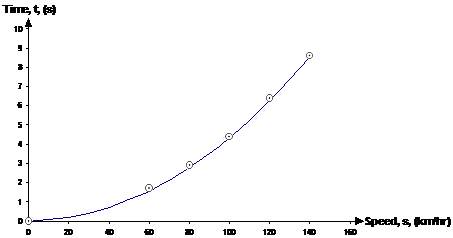
You can have quadratic, or cubic, or even higher power direct relationships.  We can go back to the car acceleration example, where the time taken to reach a certain speed was proportional to the square of the car’s speed:

                                                    

In mathematical terms, the proportionality constant would be 0.0004388.  We could write a general proportionality statement:

                                                            

One of the neat things you can do with higher order relationships is plot the squared or cubed values instead of just the value itself.  For instance, in the car speed graph above, we have plotted time, t versus speed, s.  We know that the relationship is that t is proportional to the square of the speed.  So one thing we can do is plot time versus the square of the speed.  We can do this by starting with our original data for the graph:

Usually I like to have the first row of the table represent the data that goes on the x-axis, and the second row to represent the y-axis data, so let’s swap them around:

We want to plot time versus the square of the speed, so let’s redo the first row, by taking the square of every value.  We should also relabel that row as well:

When we plot this graph, we get a very interesting result:

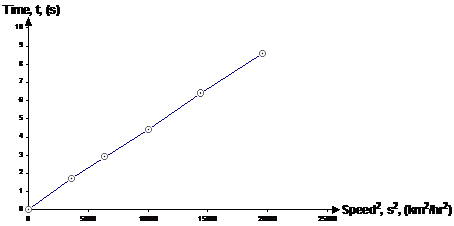
It’s basically a straight line!  This is a characteristic of proportional relationships.  If you have a relationship where , then plotting A versus B will give you a straight line.  If you have a relationship where , then plotting A versus B² will give you a straight line.  If you have a relationship where  then if you plot A versus B³ you’ll get a straight line.

This also works for fractional or negative powers.  Say we’ve got a relationship where .  This is the same as saying. If we plot a graph of A versus  then you’ll get a straight line.

To explain why this happens let’s consider one case – a direct cubic relationship between x and y:

                                                            

Because this relationship is proportional, we can write an equation relating ‘x’ and ‘y’ to each other using a constant of proportionality, k:

                                                           

If we just plotted y versus x then we’d get a graph with a curvy line in it.  Remember that you get a straight line from any equation where one thing to the power 1 equals some constant times another thing to the power 1.  The key – the powers of both variables must be the same – ‘1’.  If we replace the  with something called ‘z’ say, we get a new equation:

                                                            

This is a linear equation, which will give a straight line graph.  So by plotting ‘y’ values against ‘z’ values, which represent x³, we get a straight line.